Kilka słów o krzywych Béziera
03.06.2009 - Paweł Woźny
    Grafika komputerowa jest jednym z ciekawszych działów informatyki. O jej przydatności nie trzeba Was pewnie przekonywać (szczególnie tych, którzy sporo czasu spędzają przy grach komputerowych). Dziś trudno już wyobrazić sobie grafika, projektanta, twórcę filmów animowanych czy efektów specjalnych, który może obyć się bez komputera i zaawansowanych programów graficznych. Często metody i algorytmy wykorzystywane do tworzenia na ekranie komputera realistycznie wyglądających obiektów, scen czy animacji są bardzo skomplikowane. Istnieją jednak i takie, które są proste do zrozumienia, a mimo to pozwalają na uzyskanie ciekawych efektów. Do podstawowych narzędzi grafiki komputerowej zalicza się m.in. krzywe i powierzchnie Béziera, które są przez grafików często wykorzystywane w ich codziennej pracy. W artykule tym zajmiemy się krzywymi Béziera. Wybierzmy
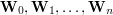 nazywamy punktami kontrolnymi (ang. control points) krzywej nazywamy punktami kontrolnymi (ang. control points) krzywej 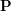 , a , a  — jej stopniem. — jej stopniem.
Musimy teraz wyjaśnić użyte oznaczenia. W podanym wzorze
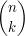 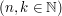 jest tzw. symbolem Newtona (ang. binomial coefficient), jest tzw. symbolem Newtona (ang. binomial coefficient),
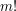 (czytamy: (czytamy:  silnia; ang. silnia; ang.  th factorial) jest iloczynem kolejnych liczb naturalnych od th factorial) jest iloczynem kolejnych liczb naturalnych od  do do  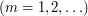 , a , a 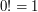 . I tak np. . I tak np.
Animacja 1.
Wydaje się to skomplikowane. Zróbmy więc prosty przykład. Przyjmijmy
![$ t\in[0,1] $](/files/tex/025317de968edba6ac0b1092780138e92cad8f14.png) , , 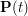 jest punktem na płaszczyźnie. Przyjmijmy jest punktem na płaszczyźnie. Przyjmijmy 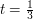 , wtedy , wtedy 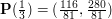 , bo , bo
Rysunek 1.
Krzywe Béziera mają wiele ciekawych własności. Krzywa
Dla danego Dla Co prawda, wartość
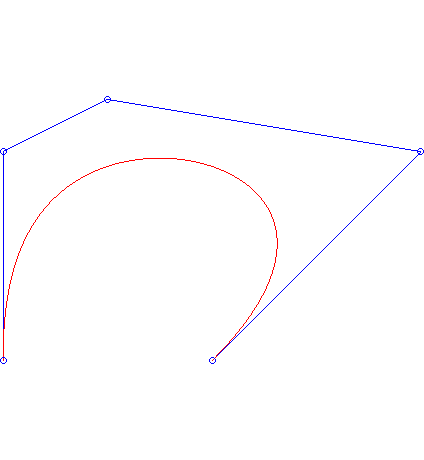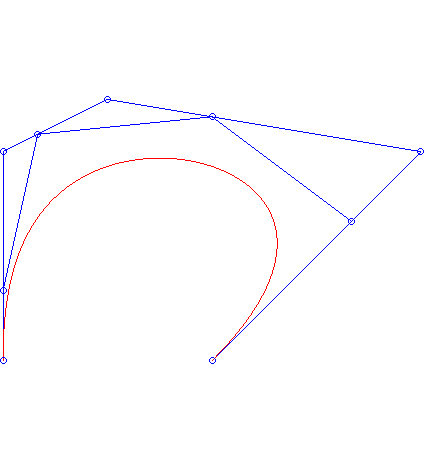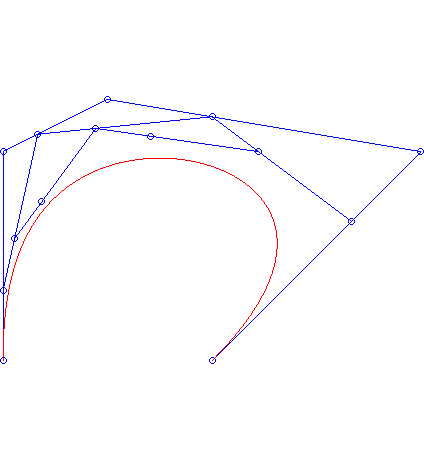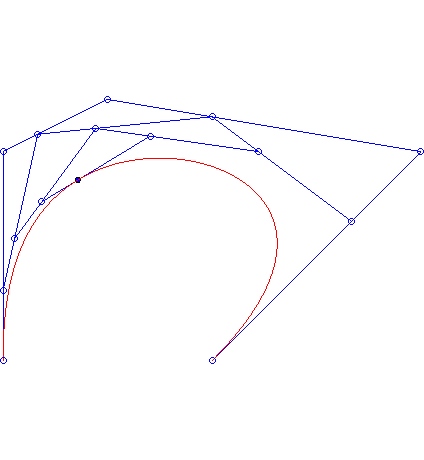
Animacja 3. Do narysowania krzywej Beziera można oczywiście wykorzystać komputer. Aby to zrobić wyznaczamy punkty
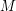 jest dostatecznie duże (np. 100). Następnie, zamiast dokładnego wykresu krzywej jest dostatecznie duże (np. 100). Następnie, zamiast dokładnego wykresu krzywej 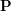 , na ekranie monitora rysujemy łamaną powstałą z połączenia ze sobą kolejno punktów , na ekranie monitora rysujemy łamaną powstałą z połączenia ze sobą kolejno punktów 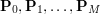 . .
Jak już wspomniałem na początku, krzywe Béziera są jednym z najczęściej używanych przez grafików komputerowych narzędziem. Przy ich pomocy można w prosty sposób modelować różne obiekty. Przeważnie używa się krzywych Béziera niewielkiego stopnia, a umiejętnie je łącząc uzyskuje się skomplikowane sceny. Animacja 4. pokazuje jak przy pomocy trzech krzywych narysować brzydkie kaczątko.
Animacja 4.
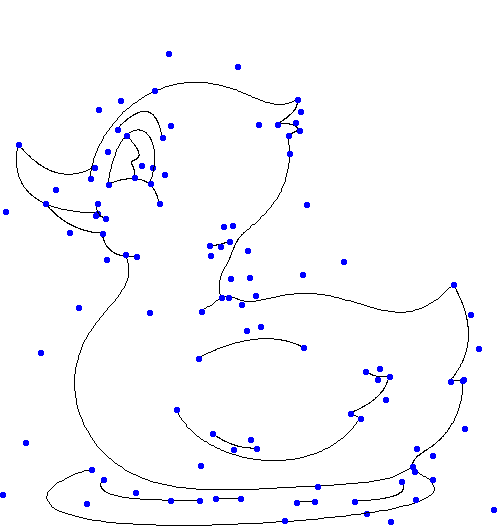
Na rysunku 2. widać kaczuszkę składającą się z 32 krzywych Béziera (punkty kontrolne wszystkich krzywych widoczne są na rysunku 3.).
Rysunek 2.
Rysunek 3.
Zachęcam do napisania programu, który pozwoli wykreślać krzywe Béziera. Można zacząć od prostego rozwiązania, polegającego na tym, że użytkownik podaje punkty kontrolne krzywej (lub krzywych) w pliku tekstowym. Ci z Was, którzy biegle już programują mogą pokusić się o przygotowanie aplikacji, która będzie łatwiejsza w obsłudze, np. punkty kontrolne będą wskazywane przy pomocy myszki, będzie je można dodawać, przesuwać, usuwać itp. Następnie wykorzystajcie swój program np. do wymodelowania karoserii wymarzonego samochodu, rysowania kaczuszek
Zadania
Paweł Woźny (7 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



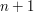 punktów na płaszczyźnie, powiedzmy
punktów na płaszczyźnie, powiedzmy 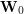 ,
, 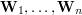 . Krzywą Béziera (ang. Bézier curve)
. Krzywą Béziera (ang. Bézier curve) ![$ {\bf P}:[0,1] \rightarrow \mathbb R^2 $](/files/tex/3b2009020cfa00ddf62b81b7e03ffbc38f4838b7.png) dla tych punktów definiujemy następującym wzorem:
dla tych punktów definiujemy następującym wzorem: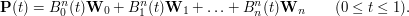
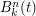
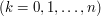 oznacza
oznacza  -ty wielomian Bernsteina stopnia
-ty wielomian Bernsteina stopnia 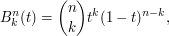
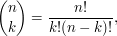
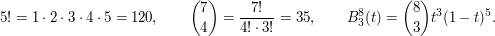
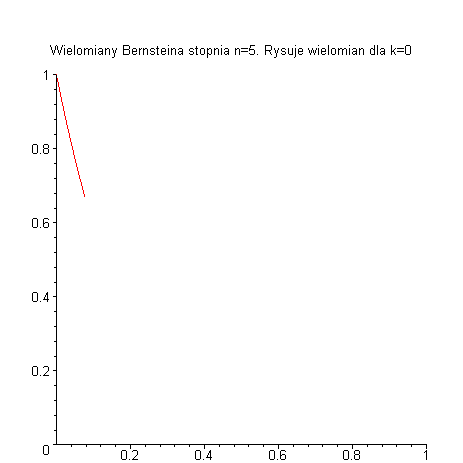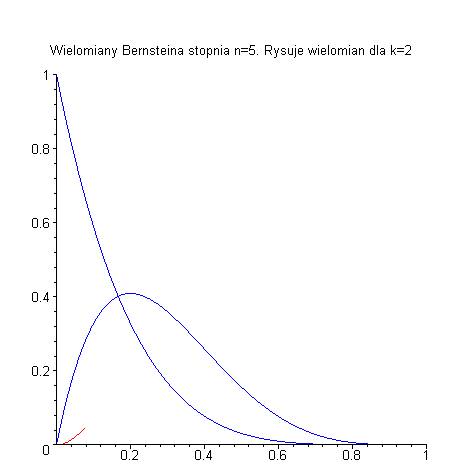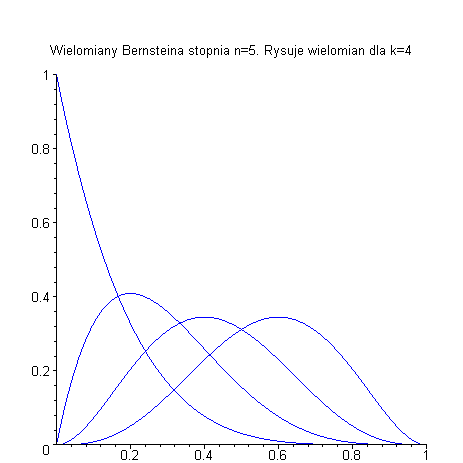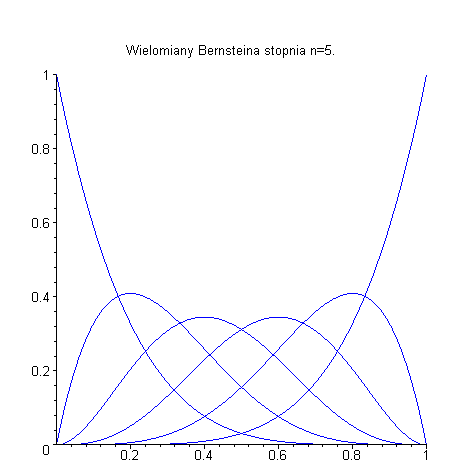
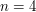 oraz
oraz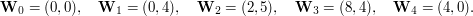
![$$\begin{array}{l}\mathbf{P}(t)=B^4_0(t)\mathbf{W}_0+B^4_1(t)\mathbf{W}_1+B^4_2(t)\mathbf{W}_2+B^4_3(t)\mathbf{W}_3+B^4_4(t)\mathbf{W}_4=\\[1.25ex] \qquad=\binom{4}{0}t^4\mathbf{W}_0+\binom{4}{1}t^3(1-t)\mathbf{W}_1+\binom{4}{2}t^2(1-t)^2\mathbf{W}_2+\binom{4}{3}t(1-t)^3\mathbf{W}_3+\binom{4}{4}(1-t)^4\mathbf{W}_4,\end{array}$$](/files/tex/00fc2fd526fbe8f7d2aa92db9356f80b7ceece60.png)
![$$\begin{array}{l}\mathbf{P}(t)=B^4_0\left(\frac{1}{3}\right)\mathbf{W}_0+B^4_1\left(\frac{1}{3}\right)\mathbf{W}_1+B^4_2\left(\frac{1}{3}\right)\mathbf{W}_2+B^4_3\left(\frac{1}{3}\right)\mathbf{W}_3+B^4_4\left(\frac{1}{3}\right)\mathbf{W}_4=\\[1.25ex] \qquad=\frac{16}{81}(0,0)+\frac{32}{81}(0,4)+\frac{8}{27}(2,5)+\frac{8}{81}(8,4)+\frac{1}{81}(4,0)=\\[1.25ex] \qquad=\left(\frac{16}{81}\cdot0+\frac{32}{81}\cdot0+\frac{8}{27}\cdot2+\frac{8}{81}\cdot8+\frac{1}{81}\cdot4,\frac{16}{81}\cdot0+\frac{32}{81}\cdot4+\frac{8}{27}\cdot5+\frac{8}{81}\cdot4+\frac{1}{81}\cdot0\right)=\\[1.25ex] \qquad=\left(\frac{116}{81},\frac{280}{81}\right).\end{array}$$](/files/tex/d07ce45109d6cbb402df26aa93a19bd47f4360b1.png)
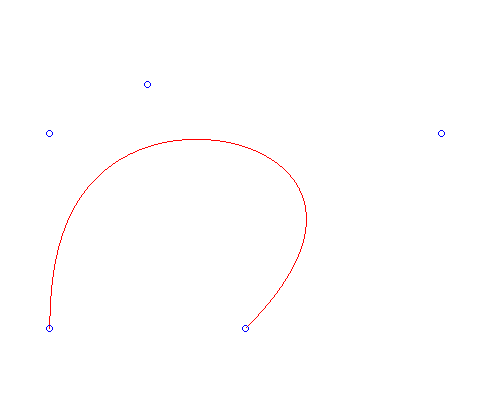
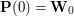 , a kończy — w punkcie
, a kończy — w punkcie 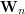 , bo
, bo 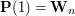 . Cała krzywa znajduje się w otoczce wypukłej (ang. convex hull) swoich punktów kontrolnych, tj. w najmniejszym wielokącie wypukłym zawierającym punkty
. Cała krzywa znajduje się w otoczce wypukłej (ang. convex hull) swoich punktów kontrolnych, tj. w najmniejszym wielokącie wypukłym zawierającym punkty 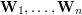 , co można zaobserwować na animacji 2. (zobacz też zadanie 3.). Własność ta ma duże znaczenie praktyczne. Pozwala ona bowiem stwierdzić w jakim obszarze znajduje się wykres krzywej. Wykorzystuje się to np. przy sterowaniu robotami pracującymi w halach fabrycznych. Ruch ich ramion jest często opisany właśnie krzywymi Béziera. Wykorzystując własność otoczki wypukłej można roboty zaprogramować tak, aby mieć pewność, że nie dojdzie do kolizji ich ramion.
, co można zaobserwować na animacji 2. (zobacz też zadanie 3.). Własność ta ma duże znaczenie praktyczne. Pozwala ona bowiem stwierdzić w jakim obszarze znajduje się wykres krzywej. Wykorzystuje się to np. przy sterowaniu robotami pracującymi w halach fabrycznych. Ruch ich ramion jest często opisany właśnie krzywymi Béziera. Wykorzystując własność otoczki wypukłej można roboty zaprogramować tak, aby mieć pewność, że nie dojdzie do kolizji ich ramion. 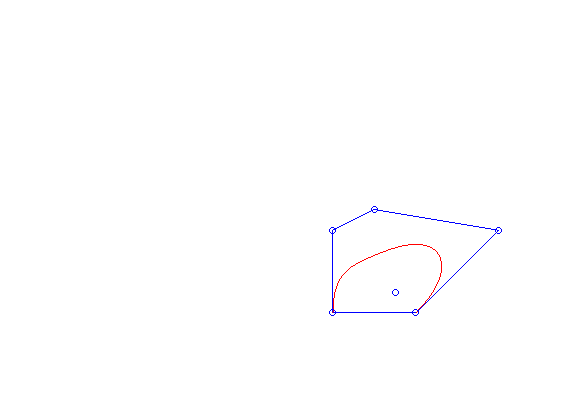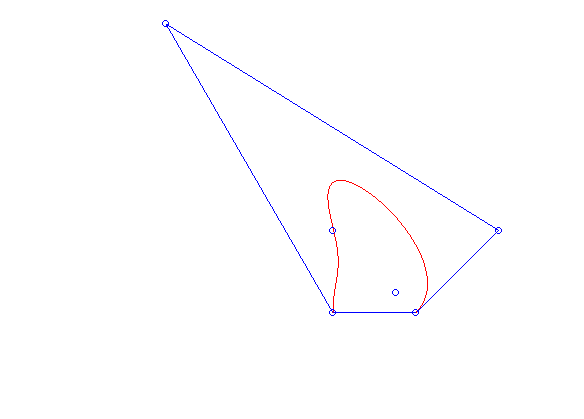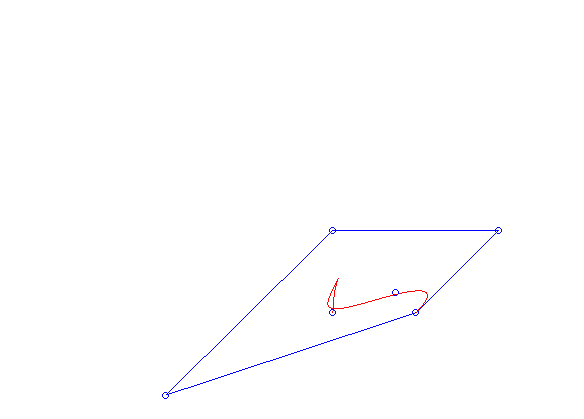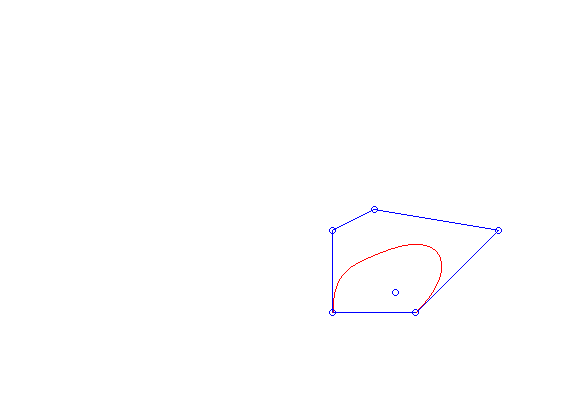
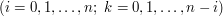 w następujący sposób rekurencyjny:
w następujący sposób rekurencyjny: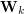
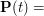
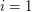 podany algorytm wyznacza
podany algorytm wyznacza  do
do 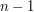 ), dla
), dla 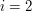 natomiast
natomiast 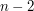 ), przy
), przy 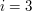 , obliczamy
, obliczamy 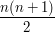 . Tak więc liczba wykonanych instrukcji przypisania (
. Tak więc liczba wykonanych instrukcji przypisania (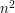 . Informatycy powiedzą, że złożoność (ang. complexity) tego algorytmu wynosi
. Informatycy powiedzą, że złożoność (ang. complexity) tego algorytmu wynosi 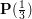 .
.
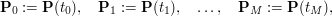
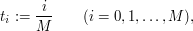
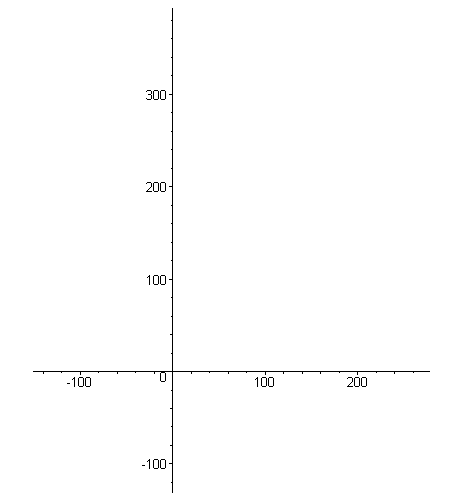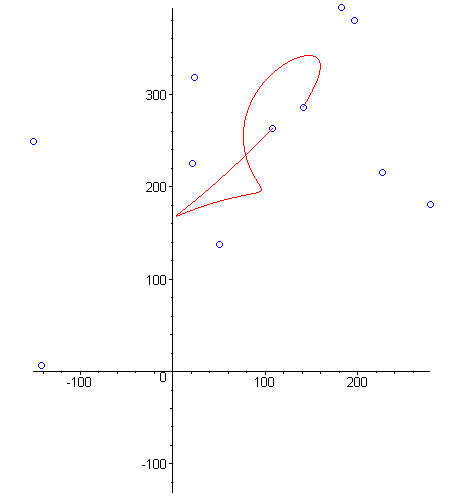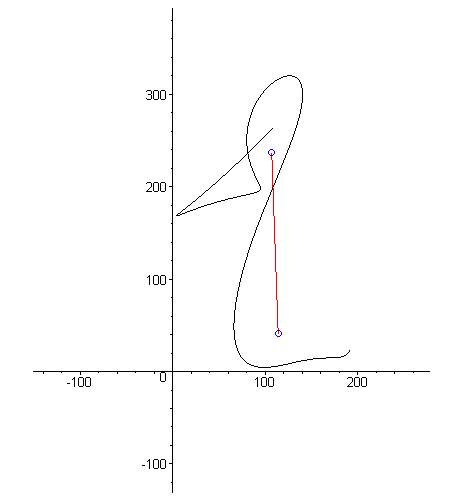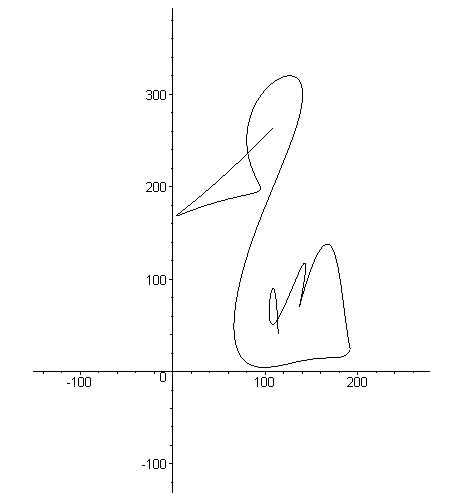

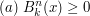 dla
dla ![$ x\in[0,1] $](/files/tex/7fd396542fa912d400b4f91c0d6d0c99df89b919.png) ,
,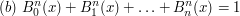 dla każdego
dla każdego 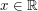 .
.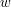 podany w postaci naturalnej (potęgowej), tzn.
podany w postaci naturalnej (potęgowej), tzn.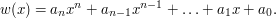
 , wartość
, wartość 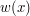 można obliczać za pomocą następującego algorytmu Hornera:
można obliczać za pomocą następującego algorytmu Hornera: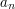
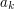
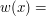
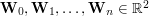 . Jaką złożoność ma Twój algorytm?
. Jaką złożoność ma Twój algorytm?

