Runda 24 (Basic) - Hamak
20.06.2011 - Damian Rusak
 Zadanie tygodnia runda 24; kategoria Basic Limit czasowy: 1s; Limit pamięciowy: 32MB HamakNadchodzi lato i cóż przyjemniejszego niż położyć się na hamaku w ogrodzie? Adam postanowił wypocząć i zawiesić hamak w swoim sadzie. Możemy myśleć o sadzie Adama jak o płaszczyźnie - w punktach o współrzędnych całkowitych rosną drzewa. Hamak może być rozpięty pomiędzy dowolną parą, ma jednak ustaloną długość - można go rozwiesić jeśli dwa drzewa są oddalone dokładnie o jego długość. Hamak traktujemy w tym przypadku jako odcinek. Niestety może się zdarzyć tak, że pewne drzewa są na drodze hamaka - jeśli punkt reprezentujący drzewo leży na odcinku reprezentującym hamak (ale nie na jednym z jego końców) to takie drzewo trzeba wyciąć. Adam nie chce wycinać wielu drzew - prosi Cię o znalezienie takiego rozpięcia hamaku, które zminimalizuje liczbę drzew, które trzeba wyciąć. Wejście Pierwsza linia wejścia zawiera jedną liczbę całkowitą Wyjście: Dla każdego zestawu danych należy wypisać jedną liczbę całkowitą w jednej linii - najmniejszą liczbę drzew, które trzeba wyciąć przy wieszaniu hamaka. Wejście: 2 13 10 Wyjście: 0 1 Wyjaśnienie - pierwszy przypadek dotyczy rozwieszenia na przykład na punktach (4,5) i (16,10), a drugi na przykład na punktach (3,2) i (9,10) (wtedy punkt (6,6) leży na odcinku reprezentującym hamak).
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 - liczbę zestawów danych. (
- liczbę zestawów danych. (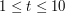 ) Każdy zestaw danych składa się z jednej liczby całkowitej
) Każdy zestaw danych składa się z jednej liczby całkowitej  - długości hamaka (
- długości hamaka (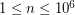 ).
).

