Runda 22 [Hard] - Malarz
06.06.2011 - Damian Rusak
 
Zadanie tygodnia runda 22; kategoria Hard Limit czasowy: 1s; Limit pamięciowy: 64MB MalarzPaweł jest malarzem. Otrzymał ostatnio zlecenie pomalowania ściany w miejscowym sklepie. Ściana ma kształt prostokąta. Zadanie byłoby proste, gdyby nie to, że na ścianie zawieszono wiele półek - oczywiście Paweł nie powinien ich zbrukać farbą, a właściciel nie zgadza się na ich zdjęcie na czas malowania tłumacząc się dużą ilością czasu potrzebną na taką operację. Paweł postanowił więc pomalować ścianę, na której wiszą półki. Półki możemy sobie wyobrażać jako prostokąty o bokach równoległych do boków ściany. Paweł chce skończyć pracę jak najszybciej, zatem planuje wybrać jak największy pędzel. Można takim pędzlem malować pionowo lub poziomo - pociągnięcia pędzla mogą być dowolnie długie (zobacz rysunek). Pędzel nie może przechodzić po prostokątach reprezentujących półki bądź poza granicami ściany, za to może przylegać do dowolnej półki lub ściany. Pomóż Pawłowi odpowiedzieć na pytanie - jaka jest największa szerokość pędzla, którym da się pomalować całą ścianę (czyli powierzchnię prostokąta bez półek) . Możesz założyć, że powierzchnia do pomalowania będzie niepusta. Na poniższym rysunku na żółto oznaczono pociągnięcia pędzla, na czarno półki.
Wejście: Pierwsza linia wejścia zawiera dwie liczby całkowite Wyjście: Wyjście powinno zawierać jedną liczbę całkowitą - największą możliwą szerokość pędzla, przy której można pomalować całą powierzchnię prostokąta z wyłączeniem półek. Przykład: Wejście: 4 6 XOOOXX XOOOOX OOXOOX XOOOOX Wyjście: 2 Przykład: Wejście: 4 6 XOOOXX XOOOOX XXXOOX XOOOOX Wyjście:
3
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




 i
i  - odpowiednio wysokość i szerokość ściany. (
- odpowiednio wysokość i szerokość ściany. (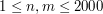 ). W kolejnych
). W kolejnych 

