Runda 21 [Basic] - Cyrkiel
23.05.2011 - Damian Rusak

Zadanie tygodnia runda 21; kategoria Basic Limit czasowy: 1s; Limit pamięciowy: 32MB CyrkielTwój przyjaciel zadał Ci pewną zagadkę: "Wyobraźmy sobie, że mamy na płaszczyźnie Jak dobrać Oczywiście nie możesz doczekać się rozwiązania - czy nie najłatwiej napisać program? Wejście: Pierwsza linia wejścia zawiera jedną liczbę całkowitą Wyjście: Wyjście powinno składać się z jednej liczby, podanej z dokładnością do 2 miejsc po przecinku - największego zarobku możliwego do uzyskania. Przykład: Wejście: 2 2 2 1 -5 6 5 Wyjście: 11.17 Objaśnienie: Optymalny promień to
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 okręgów, takich, że żaden z nich nie zawiera w środku początku układu współrzędnych. Wbijamy jedną nóźkę cyrkla w środek układu współrzędnych i rysujemy nasz okrąg o pewnym promieniu
okręgów, takich, że żaden z nich nie zawiera w środku początku układu współrzędnych. Wbijamy jedną nóźkę cyrkla w środek układu współrzędnych i rysujemy nasz okrąg o pewnym promieniu 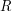 - kosztuje nas to dokładnie
- kosztuje nas to dokładnie 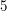 , za każdy, który nasz okrąg zawiera w sobie całkowicie (środek danego okręgu jest w naszym okręgu i oba mogą się stykać lecz nie przecinać) otrzymujemy
, za każdy, który nasz okrąg zawiera w sobie całkowicie (środek danego okręgu jest w naszym okręgu i oba mogą się stykać lecz nie przecinać) otrzymujemy 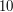 .
.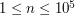 ) Kolejne
) Kolejne 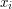
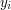 oraz
oraz 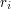 - odpowiednio współrzędne środka okręgu oraz jego promień. (
- odpowiednio współrzędne środka okręgu oraz jego promień. (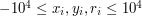 ).
). 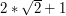 - pokrywamy wtedy w pełni pierwszy okrąg i przecinamy się z drugim, dostając
- pokrywamy wtedy w pełni pierwszy okrąg i przecinamy się z drugim, dostając 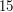 minus wielkość promienia. Nie opłaca się jednak pokrywać całego drugiego okręgu.
minus wielkość promienia. Nie opłaca się jednak pokrywać całego drugiego okręgu.

