Runda 21 [Hard] - Studnie
23.05.2011 - Damian Rusak
 
Zadanie tygodnia runda 21; kategoria Hard Limit czasowy: 2s; Limit pamięciowy: 64MB StudnieW pewnej dalekiej krainie ludzie od wieków darzą wielkim i nieprzemijającym szacunkiem studnie. Te niepozorne dziury w ziemi pozwalają przeżyć na niegościnnych terenach niemal pozbawionych wody. Nie jest to jedyna przyczyna - studnie zawierają w sobie zatopione niegdyś skarby. Ekipa ekspedycyjna postanowiła zbadać pewną grupę studni aby przekonać się, co kryją w środku. W każdej ze studni może znajdować się wiele cennych przedmiotów. Ekipa posiada ze sobą jednego robota i naraz może wydobywać jedynie jeden skarb z pewnej studni - do tego zawsze najlżejszy z nich, którego wyjęcie prowadzi zatem do najmniejszej liczby komplikacji. Ponadto prace na głębokości sprawiają, że gdzieniegdzie grunt staje się bardziej miękki i niektóre studnie podziemnymi korytarzami łączą się ze sobą w jedną. Na szczęście ekipa dysponuje sprzętem pozwalającym do sprawnie wykryć. Jeśli dwie studnie się łączą uznajemy je odtąd za jedną, a spoczywające w nich przedmioty ulegają wymieszaniu. Czy otrzymując listę studni i zatopionych w nich przedmiotów na początku ekspedycji wraz z informacjami o wyciąganiu przedmiotów ze studni i łączeniu się studni przez podwodne korytarze jesteś w stanie pomóc pracownikom i przewidzieć, jakie przedmioty będą wyciągali? Wejście: Pierwsza linia wejścia dwie liczby całkowite 1. 2. Wyjście: Dla każego zapytania pierwszego typu należy wypisać w jednej linii wagę przedmiotu wyłowionego przez robota - najtańszego przedmiotu należącego do badanego systemu studni. Jeśli w systemie brak jest już przedmiotów, należy wypisać -1. Przykład: Wejście: 4 6 4 2 1 3 1 2 2 1 3 2 2 1 1 1 1 4 1 4 Wyjście: 2 1 3 -1 Objaśnienie: pierwsze zapuszczenie się robota do studni numer dwa skutkuje usunięciem z niej przedmiotu o wadze 2. Następnie łączone są odpowiednio studnie 1 3, oraz w kolejnym kroku systemy studni 1,3 z 2. Kolejna operacja wyciąga więc najlżejszy niewyciągnięty przedmiot z systemu składającego się ze studni 1,2,3 - jest to przedmiot o wadze 1. Kolejne dwie operacje najpierw opróżniają studnię nr 4 wyciągając przedmiot o wadze 3 po czym robot nie jest w stanie nic więcej wyłowić ze studni nr 4.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 oraz
oraz  - odpowiednio liczbę studni na początku eksploatacji oraz liczbę komend do wykonania. (
- odpowiednio liczbę studni na początku eksploatacji oraz liczbę komend do wykonania. (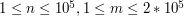 ) Kolejna linia zawiera opis poszczególnych studni - na początku każda studnia zawiera w swym środku dokładnie jeden przedmiot -
) Kolejna linia zawiera opis poszczególnych studni - na początku każda studnia zawiera w swym środku dokładnie jeden przedmiot -  -ta liczba tej linii oznacza wagę
-ta liczba tej linii oznacza wagę 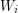 przedmiotu w
przedmiotu w  do
do 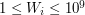 ) W kolejnych
) W kolejnych  - oznacza, że robot zapuścił się do systemu połączonych studni, w którego skład wchodzi studnia numer
- oznacza, że robot zapuścił się do systemu połączonych studni, w którego skład wchodzi studnia numer 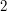

 - oznacza, że połączeniu uległy systemy połączonych studni, do których należały odpowiednio studnie
- oznacza, że połączeniu uległy systemy połączonych studni, do których należały odpowiednio studnie 

