Runda 19 [Hard] - Robaki reaktywacja
02.05.2011 - Damian Rusak
 
Zadanie tygodnia runda 19; kategoria Hard Limit czasowy: 1s; Limit pamięciowy: 32MB Robaki reaktywacjaCzy pamiętacie zadanie Robaki z Zawodów Stałych? Tym razem stoimy przed trudniejszym zadaniem! Na pręcie długości Robaczki są całkiem masywne (choć rozmiarem równe punktowi!) i gdy dwa spotkają się na pręcie idąc w przeciwne strony, oba w mgnieniu oka zmieniają kierunki - tak, jakby odbiły się od siebie. Jeśli jakiś robak dotrze do lewego lub prawego końca pręta, spada zeń i nie ma już po nim śladu. Zadanie, jakie nasuwa się szybko - znająć początkowe położenia robaczków na pręcie i kierunki, w których zmierzają, odpowiedz, który z nich spadnie z pręta jako ostatni? Możesz założyć, że dane będą dobrane w ten sposób, że nie dojdzie do sytuacji, w której kilka robaków spadałoby w ostatniej chwili. Wejście: Pierwsza linia wejścia zawiera dwie liczby - Wyjście: Wyjście powinno zawierać jedną liczbę - numer robaka, który spadnie z pręta jako ostatni. Robaki numerowane są od Przykład: Wejście: 4 10 1 1 5 0 7 0 8 1 Wyjście: 3
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



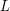 umieszczono w pewnych miejscach wiele robaczków. Każdy z nich ma określony kierunek poruszania się - w kierunku lewego końca pręta, lub w kierunku prawego końca pręta. Każdy porusza się z tą samą stałą prędkością.
umieszczono w pewnych miejscach wiele robaczków. Każdy z nich ma określony kierunek poruszania się - w kierunku lewego końca pręta, lub w kierunku prawego końca pręta. Każdy porusza się z tą samą stałą prędkością. oraz
oraz 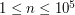 ,
, 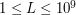 ). W kolejnych
). W kolejnych 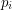
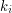 - odpowiednio położenie i kierunek robaczka. Pręt traktujemy jak odcinek
- odpowiednio położenie i kierunek robaczka. Pręt traktujemy jak odcinek ![$ [0,L] $](/files/tex/1bba2aefd75ea92b4cfe7895ba16707319a1abf5.png) . Wartość
. Wartość 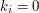 mówi, że robaczek zmierza w kierunku punktu
mówi, że robaczek zmierza w kierunku punktu  ,
, 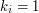 , że w kierunku punktu
, że w kierunku punktu 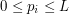 ,
, 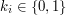 ).
).  do
do 

