Runda 19 [Basic] - Dwa ślimaki
02.05.2011 - Damian Rusak

runda 19; kategoria Basic Limit czasowy: 1s; Limit pamięciowy: 32MB Dwa ślimakiDwa ślimaki, Andrzej i Wacław, przyjaźnią się od lat. Zawsze wielką satysfakcję sprawiało im wspólne podróżowanie. Nie da się ukryć, że z powodu ich ślimaczego tempa wspólne wycieczki trwały długo, obaj planowali je więc ze wszystkimi szczegółami. Ślimaki pełzną po płaszczyźnie. Oznaczyły sobie na niej punkt z którego chcą rozpocząć podróż o współrzędnych ( Ślimaki, choć bardzo się przyjaźnią, nie znoszą spotkań na trasie - uważają, że lepiej zobaczyć się na końcu i opowiedzieć sobie o wszystkich zaznanych przygodach przy kawałku dobrego liścia. Zatem oba wyruszają z początkowego punktu, oba mają skończyć w punkcie końcowym, ale poza nimi ich trasy nie mogą się przecinać ani mieć punktów wspólnych. Ślimaki zawsze podróżują po linii prostej od jednej atrakcji do kolejnej (podobnie z punktem początkowym i końcowym). Chcą, aby ich trasy zawarły w sobie wszystkie atrkacje turystyczne. Czy pomożesz im wyznaczyć taką trasę?? Wejście: Pierwsza linia wejścia zawiera jedną liczbę całkowitą Wyjście: Wyjście powinno składać się z dwóch linii - pierwsza powinna zawierać numery atrakcji turystycznych w kolejności, w jakiej zwiedzać będzie je pierwszy ślimak, druga zaś numery zwiedzane przez drugiego ślimaka. Jeśli istnieje wiele rozwiązań, Twój program może wypisać dowolne z nich. Atrakcje numerowane są od Przykład: Wejście: 3 0 0 7 2 2 2 3 1 6 4 Wyjście: 1 3 2 Pierwszy ślimak pełznie od (0,0) do (2,2), potem do (6,4), wreszcie do (7,2). Drugi ślimak porusza się od (0,0) do (3,1), potem do (7,2). Trasy nie przecinają się ani nie posiadają punktów wspólnych poza początkiem i końcem.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



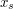 ,
, 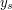 ) oraz punkt końcowy (
) oraz punkt końcowy (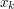 ,
, 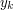 ). Wiadomo, że
). Wiadomo, że 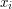 ,
, 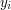 ) i wiadomo, że wszystkie punkty (wraz z początkiem i końcem) są różne i zawsze
) i wiadomo, że wszystkie punkty (wraz z początkiem i końcem) są różne i zawsze 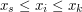 .
.  - liczbę atrkacji turystycznych (
- liczbę atrkacji turystycznych (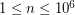 ). W kolejnej linii znajdują się liczby całkowite
). W kolejnej linii znajdują się liczby całkowite ![$ \left[0,10^{9}\right] $](/files/tex/c79d4284cb1a15bcacc2a17b010e8dead94b3e1d.png) ). W kolejnych
). W kolejnych  . (z zakresu
. (z zakresu  do
do 

