Zadanie tygodnia
runda 16; kategoria Hard
Limit czasowy: 1s; Limit pamięciowy: 32MB
Spacer po kostce
Wiemy dobrze czym są odcinek, kwadrat albo sześcian. Jak jednak wyglądałaby analogiczna figura w  wymiarach?
wymiarach?
W  wymiarowej przestrzeni żyje sobie robaczek Adam. Ciężko jest sobie wyobrazić
wymiarowej przestrzeni żyje sobie robaczek Adam. Ciężko jest sobie wyobrazić  - wymiarową przestrzeń, zatem Adam wpadł na pomysł, jak opowiadać znajomym z niższych wymiarów o swoim świecie. Adam mieszka w hiperkostce - możemy myśleć o takim obiekcie jak o grafie, który ma
- wymiarową przestrzeń, zatem Adam wpadł na pomysł, jak opowiadać znajomym z niższych wymiarów o swoim świecie. Adam mieszka w hiperkostce - możemy myśleć o takim obiekcie jak o grafie, który ma 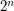 wierzchołków (dla przestrzeni jednowymiarowej jest to odcinek, dla dwuwymiarowej kwadrat, dla trójwymiarowej sześcian itd.) numerowanych liczbami od
wierzchołków (dla przestrzeni jednowymiarowej jest to odcinek, dla dwuwymiarowej kwadrat, dla trójwymiarowej sześcian itd.) numerowanych liczbami od  do
do 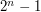 . Dwa wierzchołki takiego grafu są połączone krawędzią nieskierowaną, jeśli ich numery zapisane w systemie binarnym różnią się dokładnie na jednej pozycji. (na przykład dla
. Dwa wierzchołki takiego grafu są połączone krawędzią nieskierowaną, jeśli ich numery zapisane w systemie binarnym różnią się dokładnie na jednej pozycji. (na przykład dla 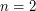 można ponumerować wierzchołki kwadratu liczbami od
można ponumerować wierzchołki kwadratu liczbami od  do
do 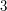 - wtedy połączone są pary wierzchołków
- wtedy połączone są pary wierzchołków 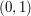 ,
, 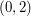 ,
, 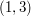 ,
, 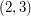 , gdyż ich zapisy binarne to
, gdyż ich zapisy binarne to 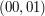 ,
, 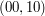 ,
, 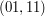 ,
, 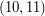 )
)
Adam uwielbia podróżować po hiperkostce i pragnie opowiedzieć nam, jak wygląda jego podróż. Chciałby wystartować w wierzchołku o numerze  i przejść po wszystkich wierzchołkach hiperkostki, tak, aby w każdym z nich być dokładnie jeden raz. Oczywiście podróż taka może przebiegać jedynie po krawędziach łączących wierzchołki. Jednak ma problem z opisaniem takiej podróży i poprosił Cię o pomoc.
i przejść po wszystkich wierzchołkach hiperkostki, tak, aby w każdym z nich być dokładnie jeden raz. Oczywiście podróż taka może przebiegać jedynie po krawędziach łączących wierzchołki. Jednak ma problem z opisaniem takiej podróży i poprosił Cię o pomoc.
Wejście:
Jedyna linia wejścia zawiera dwie liczby  oraz
oraz  - odpowiednio wymiar przestrzeni w której wędruje Adam, oraz numer wierzchołka z którego pragnie rozpocząć podróż. (
- odpowiednio wymiar przestrzeni w której wędruje Adam, oraz numer wierzchołka z którego pragnie rozpocząć podróż. (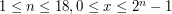 ).
).
Wyjście:
Wyjście powinno składać się z jednej linii, zawierającej 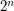 liczb - numerów kolejnych wierzchołków (poczynając od
liczb - numerów kolejnych wierzchołków (poczynając od  ) po których kroczył będzie Adam, tak, że każde dwa kolejne numery odpowiadają wierzchołkom połączonym krawędzią i każdy numer ze zbioru
) po których kroczył będzie Adam, tak, że każde dwa kolejne numery odpowiadają wierzchołkom połączonym krawędzią i każdy numer ze zbioru 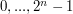 występuje dokładnie raz. Jeśli możliwe jest wiele odpowiedzi, Twój program może wypisać dowolną z nich.
występuje dokładnie raz. Jeśli możliwe jest wiele odpowiedzi, Twój program może wypisać dowolną z nich.
Przykład:
Wejście:
2 1
Wyjście:
1 0 2 3
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.





 wymiarach?
wymiarach? 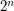 wierzchołków (dla przestrzeni jednowymiarowej jest to odcinek, dla dwuwymiarowej kwadrat, dla trójwymiarowej sześcian itd.) numerowanych liczbami od
wierzchołków (dla przestrzeni jednowymiarowej jest to odcinek, dla dwuwymiarowej kwadrat, dla trójwymiarowej sześcian itd.) numerowanych liczbami od  do
do 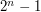 . Dwa wierzchołki takiego grafu są połączone krawędzią nieskierowaną, jeśli ich numery zapisane w systemie binarnym różnią się dokładnie na jednej pozycji. (na przykład dla
. Dwa wierzchołki takiego grafu są połączone krawędzią nieskierowaną, jeśli ich numery zapisane w systemie binarnym różnią się dokładnie na jednej pozycji. (na przykład dla 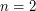 można ponumerować wierzchołki kwadratu liczbami od
można ponumerować wierzchołki kwadratu liczbami od 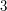 - wtedy połączone są pary wierzchołków
- wtedy połączone są pary wierzchołków 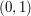 ,
, 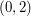 ,
, 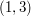 ,
, 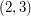 , gdyż ich zapisy binarne to
, gdyż ich zapisy binarne to 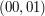 ,
, 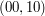 ,
, 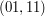 ,
, 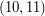 )
) i przejść po wszystkich wierzchołkach hiperkostki, tak, aby w każdym z nich być dokładnie jeden raz. Oczywiście podróż taka może przebiegać jedynie po krawędziach łączących wierzchołki. Jednak ma problem z opisaniem takiej podróży i poprosił Cię o pomoc.
i przejść po wszystkich wierzchołkach hiperkostki, tak, aby w każdym z nich być dokładnie jeden raz. Oczywiście podróż taka może przebiegać jedynie po krawędziach łączących wierzchołki. Jednak ma problem z opisaniem takiej podróży i poprosił Cię o pomoc.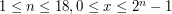 ).
).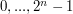 występuje dokładnie raz. Jeśli możliwe jest wiele odpowiedzi, Twój program może wypisać dowolną z nich.
występuje dokładnie raz. Jeśli możliwe jest wiele odpowiedzi, Twój program może wypisać dowolną z nich.

