Grupowanie danych to popularne w ostatnich latach zagadnienie informatyczne o bardzo szerokich zastosowaniach. Na czym ono polega?
Wyobraźmy sobie zbiór pewnych obiektów, na przykład zbiór zerwanych kwiatów. Obiekty opisane są przez pewną liczbę cech, w przypadku kwiatów mogą to być długość i szerokość płatka oraz długość i szerokość listka (rysunek 1). Grupowanie danych polega na podziale zbioru danych obiektów na grupy, w taki sposób, aby obiekty należące do tej samej grupy były do siebie jak najbardziej podobne, zaś obiekty należące do różnych grup były od siebie jak najbardziej różne. Innymi słowy, każde dwa obiekty z tej samej grupy powinny mieć zbliżone wartości poszczególnych cech, zaś każde dwa obiekty z różnych grup powinny mieć odległe wartości poszczególnych cech.

Rysunek 1. Każdy kwiat z naszego zbioru może zostać opisany przez cztery cechy: długość i szerokość płatka oraz długość i szerokość listka.
Jeśli nasze obiekty opisywane byłyby przez dwie cechy, moglibyśmy zaznaczyć je w dwuwymiarowym układzie współrzędnych (pierwsza cecha – oś X, druga cecha – oś Y) i wzrokowo podzielić je na grupy (przykład widoczny jest na rysunku 2). W przypadku trzech cech, moglibyśmy pokusić się o narysowanie danych w trójwymiarowym układzie współrzędnych (osie X, Y, Z) i przy dobrej wyobraźni przestrzennej moglibyśmy wzrokowo wyodrębnić grupy danych. Problem jest jednak trudniejszy w przypadku większej liczby cech.
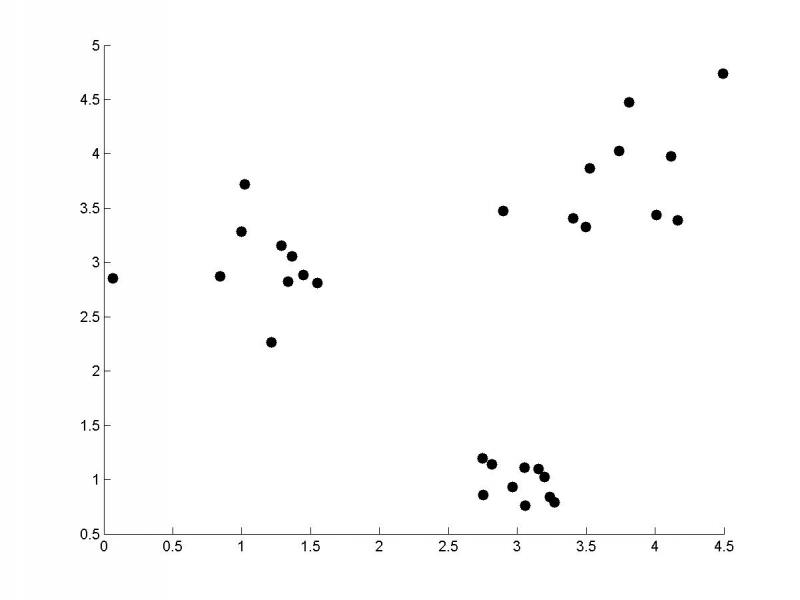
Rysunek 2. Widoczne na rysunku dane można wzrokowo podzielić na trzy grupy.
Jedną z prostych metod rozwiązania takiego problemu jest algorytm k-means. Służy on do podziału obiektów na k grup, gdzie k jest z góry zadaną liczbą. Algorytm rozpoczyna się od wyboru k punktów zwanych centrami grup (rysunek 3a). Centra są początkowo ustawione losowo, a w trakcie działania algorytmu są przesuwane tak, aby najlepiej oddawać właściwości danych. Następnie, dla każdego punktu danych obliczana jest jego odległość od każdego z centrów grup i określane jest najbliższe mu centrum grupy (jeśli nie ma jednego najbliższego centrum – czyli kilka centów jest równoodległych od analizowanego punktu danych – to wybierane jest jedno z tych centrów w sposób losowy). Każdy punkt danych zostaje więc przypisany do jednego z centrów grup. Punkty danych przypisane do tego samego centrum grupy tworzą grupę (rysunek 3b). Po podziale punktów danych na grupy, dla każdej grupy wyznaczana jest nowa pozycja centrum grupy – środek ciężkości wszystkich punktów należących do danej grupy (czyli punkt o współrzędnych będących średnimi arytmetycznymi odpowiednich współrzędnych wszystkich punktów należących do danej grupy) (rysunek 3c). Po przesunięciu centrów grup na nowe pozycje, odległości między punktami danych a centrami grup zmieniają się, więc dla niektórych punktów danych może zmienić się przypisane mu centrum grupy. Dla każdego punktu danych jest więc na nowo wyznaczane najbliższe mu centrum danych i cała operacja jest powtarzana wielokrotnie, aż do ustabilizowania się położenia centrów grup, czyli momentu, w którym nie następuje już przesunięcie żadnego z centrów grup (rysunek 3d). Po zakończeniu algorytmu, dane zostają podzielone na grupy według ostatniego położenia centrów grup.
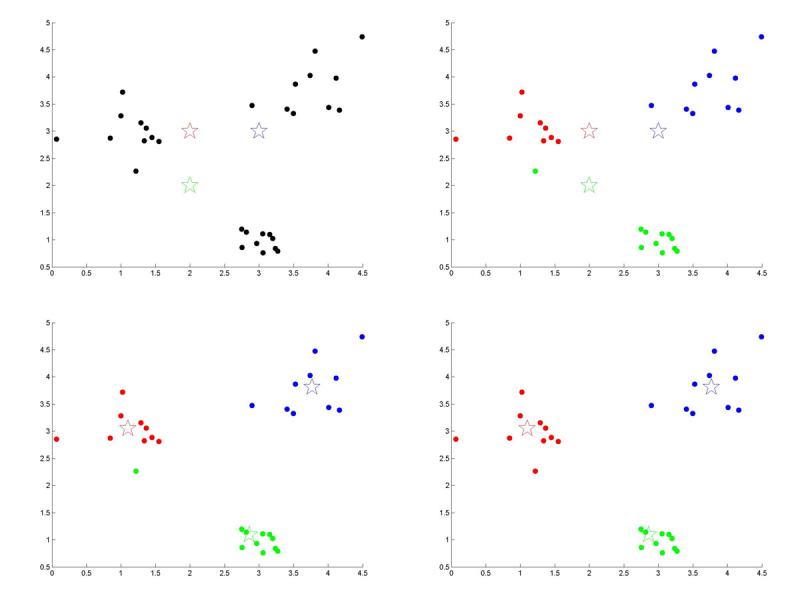
Rysunek 3. (a) czarne punkty przedstawiają dane, trzy kolorowe gwiazdki przedstawiają losowo ustawione centra grup (b) każdy punkt danych zostaje przypisany do najbliższego mu centrum grupy i pokolorowany na jego kolor (c) centra grup zostają przesunięte na nowe pozycje – środki ciężkości zbiorów punktów w odpowiednim kolorze (d) punkty danych są powtórnie dzielone na grupy, jeden z punktów zmienił kolor
Zauważmy, że jednym z wymagań algorytmu k-means jest podanie liczby grup na które chcemy podzielić dane. W przykładzie przedstawionym na rysunku 3, przyjęliśmy k = 3 i wybór ten okazał się dobry. W praktyce zazwyczaj wykonuje się algorytm k-means dla różnych k, na przykład kolejnych liczb z zakresu od 2 do 50, i po wykonaniu serii eksperymentów wybiera się takie k, które doprowadziło do najlepszego grupowania danych (punkty tej samej grupy są do siebie jak najbardziej zbliżone, zaś punkty różnych grup są od siebie jak najbardziej oddalone). Jakość grupowania można mierzyć wieloma metodami, jedną z nich może być stosunek średniej odległości między dwoma punktami z tej samej grupy do średniej odległości między dwoma punktami z różnych grup.
Grupowanie danych pozwala nam podzielić dane na pewną liczbę grup. Niekoniecznie jednak ten podział musi być zgodny z naszymi intencjami. Wiedząc na przykład, że zrywane na łące kwiaty były trzech różnych gatunków, moglibyśmy oczekiwać, że dane zostaną podzielone na trzy grupy odpowiadające właśnie tym gatunkom. Nie musi się tak stać. Algorytm grupowania łączy bowiem dane w grupy biorąc pod uwagę jedynie ich opis przez określone cechy, na przykład długość i szerokość płatka oraz długość i szerokość listka, a te cechy nie muszą wcale być różne dla różnych gatunków kwiatów.
Zobaczmy jeszcze jak algorytm k-means działa w praktyce. Zajmiemy się klasycznym przykładem danych, opublikowanych przez Fishera w 1936 roku, które opisują 150 kwiatów, po 50 kwiatów z 3 różnych gatunków irysa (iris setosa, iris virginica oraz iris versicolor) . Każdy kwiat opisany jest przez cztery cechy: długość i szerokość płatka oraz długość i szerokość listka (rysunek 1). Ponieważ dane są czterowymiarowe, mielibyśmy problem z wizualnym podziałem ich na grupy, dlatego więc użyjemy algorytmu k-means.
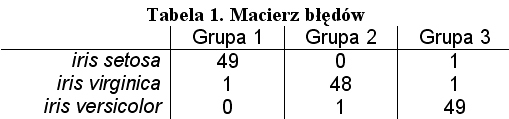
Algorytm k-means zastosowaliśmy z parametrem k = 3 i wykonaliśmy 100 jego iteracji otrzymując podział danych na 3 grupy. Czy grupy danych, które dostaliśmy odpowiadają trzem gatunkom irysa? Chociaż do znalezienia podziału na grupy, algorytm k-means używał tylko informacji o wymiarach kwiatów, zakładając, że kwiaty różnych gatunków różnią się znacznie swoimi wymiarami (a nie na przykład możliwymi kolorami płatków, które nie są ujęte w naszych danych), oczekiwalibyśmy, że otrzymane trzy grupy danych powinny być zgodne z trzema gatunkami irysów. Sprawdźmy to przy użyciu macierzy błędów.
Macierz błędów (ang. confusion matrix) przedstawia tabela 1. Wiersze macierzy odpowiadają gatunkowi irysa, do którego należał punkt danych. Kolumny macierzy odpowiadają grupie, do której został zakwalifikowany punkt danych. Elementy macierzy określają liczbę punktów danych odpowiadających gatunkowi irysa określonemu w nagłówku wiersza przypisanych do grupy danych określonej w nagłówku kolumny. Zauważmy dużą zgodność między grupami danych a gatunkami irysów. Pomijając niewielkie błędy, możemy stwierdzić, że pierwsza grupa danych odpowiada iris setosa (chociaż jeden iris setosa został przypisany do grupy trzeciej, zaś w grupie pierwszej znalazł się jeden iris virginica), druga grupa danych odpowiada iris virginica, zaś trzecia grupa danych odpowiada iris versicolor.
Algorytm k-means jest jednym z prostszych algorytmów grupowania danych. Wśród innych popularnych algorytmów grupowania danych można znaleźć algorytmy oparte na metodach statystycznych, sieciach neuronowych lub algorytmach ewolucyjnych. Jest to jednak już temat na zupełnie inny artykuł.
Zadania dla czytelnika:
1. Centra grup w algorytmie k-means są początkowo ustawiane losowo. Jaki wpływ na wynik działania algorytmu ma początkowe wylosowane ustawienie centrów ? Czy warto uruchamiać algorytm k-means kilkakrotnie ?
2. Algorytm k-means przy wyznaczaniu dla poszczególnych punktów danych najbliższych im centrów grup używa odległości euklidesowej. Jakie inne miary odległości w przestrzeni danych można zastosować ? Jaki wpływ może mieć to na grupowanie danych ?
3. Spróbuj znaleźć w internecie dane opisujące pogodę w wybranym miejscu świata w różnych dniach roku (na przykład temperaturę, ciśnienie, prędkość wiatru i wysokość opadów we Wrocławiu w kolejnych dniach 2008 roku). Pogrupuj dni używając algorytmu k-means. Czy można powiedzieć czemu odpowiadają powstałe grupy ?
4. Dla danych z zadania 3, znajdź podział dni na 4 grupy, a następnie sprawdź w jakim stopniu powstałe grupy dni odpowiadają 4 porom roku. Najwygodniej sprawdzić to sporządzając macierz błędów (ang. confusion matrix).
Piotr LipińskiInstytut Informatyki Uniwersytetu Wrocławskiegolipinski@ii.uni.wroc.pl












