Runda 14 [Hard] - Łańcuchy
07.03.2011 - Damian Rusak
 
Zadanie tygodnia runda 14; kategoria Hard Limit czasowy: 3s; Limit pamięciowy: 64MB
ŁańcuchyArtur znalazł atrakcyjną posadę w spawalni łańcuchów. Jego praca jest satysfakcjonująca i pasjonująca - przydzielono go do sekcji spawania obręczy. Każdy z łańcuchów w spawalni ma określoną długość. Obręczą nazwiemy ciąg łańcuchów Artur otrzymał do zespawania cały zestaw łańcuchów. Zastanawia się, na ile sposobów może utworzyć z nich obręcze, tak aby każdy łańcuch należał do dokładnie jednej z nich. Dwa sposoby wyboru są różne wtedy i tylko wtedy, gdy można wskazać pewien łańcuch Wejście: Pierwsza linia wejścia zawiera jedną liczbę całkowitą Wyjście: Dla każdego zestawu danych należy w jednej linii wypisać resztę z dzielenia przez Przykład: Wejście: 2 2 10 18 5 100 200 3 3 3 Wyjście: 1 0 Wyjaśnienie: W pierwszym przypadku możemy stworzyć jedynie obręcz z łańcuchów o długościach Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



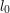 ,
, 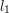 , ...,
, ..., 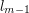 o długościach
o długościach 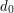 ,
, 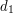 , ...,
, ..., 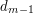
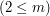 jeśli można je zespawać kolejno ze sobą oraz zespawać ostatni z łańcuchów z pierwszym. Jest to możliwe, o ile (ze względów bezpieczeństwa i dla uzyskania stabilnej obręczy) dla każdej kolejnej pary łańcuchów, które zostały ze soba zespawane ich długości różnią się co do wartości bezwględnej o co najwyżej długość pierwszego z nich. Inaczej mówiąc dla
jeśli można je zespawać kolejno ze sobą oraz zespawać ostatni z łańcuchów z pierwszym. Jest to możliwe, o ile (ze względów bezpieczeństwa i dla uzyskania stabilnej obręczy) dla każdej kolejnej pary łańcuchów, które zostały ze soba zespawane ich długości różnią się co do wartości bezwględnej o co najwyżej długość pierwszego z nich. Inaczej mówiąc dla 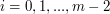 mamy
mamy 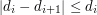 oraz
oraz 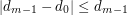 .
.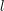 taki ,że obręcze do których należy w pierwszym i w drugim sposobie wyboru nie są tymi samymi ciągami łańcuchów (z dokładnością do przesunięcia cyklicznego -
taki ,że obręcze do których należy w pierwszym i w drugim sposobie wyboru nie są tymi samymi ciągami łańcuchów (z dokładnością do przesunięcia cyklicznego - 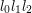 to ta sama obręcz co
to ta sama obręcz co  ). Artur poprosił Cię o pomoc. Aby ułatwić Ci zadanie dodał, że interesuje go tylko reszta z dzielenia tej liczby przez
). Artur poprosił Cię o pomoc. Aby ułatwić Ci zadanie dodał, że interesuje go tylko reszta z dzielenia tej liczby przez 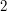 .
. - liczbę zestawów danych
- liczbę zestawów danych 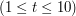 . Po niej następują opisy kolejnych zestawów danych. Każdy z nich składa się z dwóch linii - pierwsza zawiera liczbę całkowitą
. Po niej następują opisy kolejnych zestawów danych. Każdy z nich składa się z dwóch linii - pierwsza zawiera liczbę całkowitą  - liczbę łańcuchów
- liczbę łańcuchów 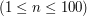 . W kolejnej linii znajduje się
. W kolejnej linii znajduje się 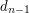 - są to długości łańcuchów.
- są to długości łańcuchów. 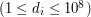 .
.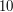 i
i 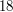 (spełniają warunek, że
(spełniają warunek, że 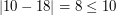 i
i 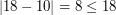 ). W drugim przypadku łańcuchy o długościach
). W drugim przypadku łańcuchy o długościach 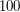 oraz
oraz 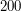 muszą zostać połaczone ze sobą, za to łańcuchy o długości
muszą zostać połaczone ze sobą, za to łańcuchy o długości 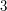 można na dwa sposoby połączyć w obręcz (pierwszy-drugi-trzeci lub pierwszy-trzeci-drugi).
można na dwa sposoby połączyć w obręcz (pierwszy-drugi-trzeci lub pierwszy-trzeci-drugi).

