Beetle
09.02.2011 - Anna Piekarska
  W 2009 roku udało mi się dostać do reprezentacji Polski na Bałtycką Olimpiadę Informatyczną. Jak większość tego typu imprez, także i ta co roku odbywa się w innym miejscu. Tym razem był to Sztokholm, a (prawie) równolegle do zawodów odywały finały ACM ICPC (a co za tym idzie, w programie było zdecydowanie więcej atrakcji niż w innych latach!). Zadaniem, które sprawiło mi najwięcej radości (chociażby dlatego, że udało mi się je rozwiązać pomimo tego, że początkowo wydawało mi się dość trudne), było beetle. Jest na tyle ciekawe, że chciałabym je Wam przedstawić. Czego od nas chcą w tym zadaniu?Danych jest Kilka bardziej lub mniej oczywistych spostrzeżeń na dobry początekJeśli w optymalnym rozwiązaniu w pewnym momencie pewne dwie krople
|
![$$t_1 = dp[left-1][right[1][time+dist(cur, left-1)]$$](/files/tex/d27e6fbb2775deeecee10086d91500403ba409f7.png) |
![$$t_2 = dp[left][right+1][0][time+dist(cur, right+1)]$$](/files/tex/02cfbecfc6dfff48f743b4ebe0c13dae8d5c903c.png) |
![$$dp[left][right][isleft][time] = m-time + max(t_1, t_2)$$](/files/tex/eccc8c6661ec74706431d050471e1b2754262ffb.png) |
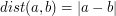 (odległość dwóch punktów) i
(odległość dwóch punktów) i 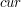 jest aktualną pozycją chrząszcza (czyli
jest aktualną pozycją chrząszcza (czyli 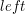 lub
lub 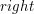 w zależności od
w zależności od 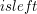 )
)
Niestety, taka złożoność nas nie satysfakcjonuje. W pesymistycznym przypadku mamy 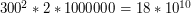 operacji czyli dużo za dużo.
operacji czyli dużo za dużo.
I co dalej?
Programowanie dynamiczne nasuwa się od razu - bo co innego? Poprzedni algorytm wygląda na dość ciekawą podstawę do ładnego i szybkiego rozwiązania. Tylko jak właściwie powinno ono wyglądać?
Rozwiązanie znalezione przez poprzedni algorytm można przedstawić na wykresie położenia 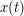 od czasu
od czasu  i zaznaczyć punkty oznaczające kolejne krople wody. Wtedy wynikiem algorytmu będzie
i zaznaczyć punkty oznaczające kolejne krople wody. Wtedy wynikiem algorytmu będzie 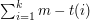 , gdzie
, gdzie  jest liczbą odwiedzonych kropli, a
jest liczbą odwiedzonych kropli, a 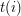 czasem odwiedzenia
czasem odwiedzenia  -tej kropli. Spróbujmy przekształcić ten wzór. Dla uproszczenia załóżmy
-tej kropli. Spróbujmy przekształcić ten wzór. Dla uproszczenia załóżmy 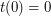 (możemy dołożyć wyimaginowany punkt i odjąć od wyniku
(możemy dołożyć wyimaginowany punkt i odjąć od wyniku  ).
).
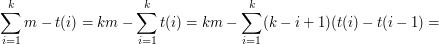 |
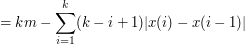 |
Na podstawie tego wzoru łatwo zauważyć, że po wybraniu liczby kropli, które zamierzamy wypić, nasz wynik prawie przestaje zależeć od  oraz czasu - wystarczy dodać do wyniku
oraz czasu - wystarczy dodać do wyniku 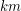 i zapomnieć o
i zapomnieć o  .
.
W nowym rozwiązaniu dynamicznym będziemy wciąż pamiętać początek i koniec przedziału już odwiedzonych punktów oraz flagę mówiącą po której stronie aktualnie jesteśmy. Tym razem jednak ostatnią wartością będzie liczba kropli, które planujemy jeszcze wypić.
Zależność dynamiczną możemy opisać wzorem:
![$$t_1 = dist(cur, left-1) * k + dp[left-1][right][1][k-1]$$](/files/tex/47fdefa53d86d8ec33461c0cb767a0231c09c17e.png) |
![$$t_2 = dist(cur, right+1) * k + dp[left][right+1][0][k-1]$$](/files/tex/931f8e62130d8a33518026557ccc133b683ff9dc.png) |
![$$dp[left][right][isleft][k] = min(t_1, t_2)$$](/files/tex/182b8eb6a5414e52f91dc18af7aae6323b644929.png) |
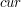 i
i 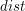 są zdefiniowane jak w poprzednim paragrafie.
są zdefiniowane jak w poprzednim paragrafie.
Daje to złożoność 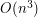 czyli w zupełności wystarczającą przy tych limitach.
czyli w zupełności wystarczającą przy tych limitach.
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 punktów na prostej osi. Startujemy wędrówkę
w punkcie 0 i poruszamy się po osi w prawo lub w lewo. Jeśli napotkamy
któryś z punktów, możemy go "wypić", czyli dodać do wyniku aktualną
wartość punktu oraz usunąć punkt. Aktualna wartość kropli to
punktów na prostej osi. Startujemy wędrówkę
w punkcie 0 i poruszamy się po osi w prawo lub w lewo. Jeśli napotkamy
któryś z punktów, możemy go "wypić", czyli dodać do wyniku aktualną
wartość punktu oraz usunąć punkt. Aktualna wartość kropli to 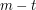 jeśli
jeśli 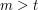 lub 0 jeśli
lub 0 jeśli 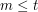 , gdzie
, gdzie  i
i  zostały już wypite, to wszystkie krople pomiędzy
zostały już wypite, to wszystkie krople pomiędzy 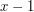 lub
lub 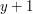 (lub nie będzie to żadna z nich i chrząszcz zakończy swój spacer).
(lub nie będzie to żadna z nich i chrząszcz zakończy swój spacer).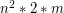 .
.

