Runda 9 [Basic] - Szosa
31.01.2011 - Damian Rusak

Zadanie Tygodnia Runda 9; kategoria Basic Limit czasowy: 1s; Limit pamięciowy: 16MB SzosaJak najszybciej dojechać z jednego miasta do drugiego? To bardzo klasyczne pytanie. Szosa łączy miasta A oraz B i przecięta jest wieloma przejazdami kolejowymi. Na szosie panuje pewne ograniczenie prędkości. Adam planuje przejechać jak najszybciej z miasta A do miasta B. Oczywiście jest odpowiedzialnym kierowcą i nigdy nie przekracza ograniczenia prędkości, jakie panuje na szosie. Przed każdym z przejazdów kolejowych Adam musi się zatrzymać (jego prędkość spada do zera, przyjmujemy, że jest w stanie zatrzymać się natychmiast, bez czasu potrzebnego na hamowanie). Samochód Adama posiada pewne stałe przyspieszenie (z lekcji fizyki wiadomo, że przyspieszenie to zmiana prędkości w czasie). Znając przyspieszenie samochodu Adama, odległość z miasta A do miasta B oraz pozycje przejazdów kolejowych na szosie odpowiedz na pytanie w jakim czasie Adam może najszybciej pokonać całą długość szosy. Wejście: Pierwsza linia wejścia zawiera cztery liczby całkowite Wyjście: Wyjście powinno składać się z jednej liczby rzeczywistej, podanej w zaokrągleniu do dwóch miejsc po przecinku - minimalnego czasu w którym Adam może dostać się z miasta A do miasta B, podanego w sekundach. Uwaga! Aby wypisać liczbę typu double z dwoma miejscami po przecinku można użyć funkcji printf z formatem %.2lf - na przykład zmienną a typu double możemy wypisać tak: printf("%.2lf", a) Przykład: Wejście: 26 2 1 4 8 24 Wyjście: 12.00 Wyjaśnienie: Pierwszy odcinek od miasta A do pierwszego przejazdu ma długość 8 metrów. Adam pokona go w 4 sekundy i tuż przed przejazdem osiągnie prędkość 4m/s. Kolejny odcinek ma długość 16 metrów i Adam pokona go w 6 sekund - po 4 sekundach przebędzie 8 metrów i będzie miał prędkość 4m/s, której nie będzie mógł przekroczyć. Wtedy pozostałe 8 metrów pokona w 2s. Od ostatniego przejazdu do miasta B odległość to 2 metry, którą Adam pokona w 2 sekundy. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 ,
,  ,
,  oraz
oraz  - kolejno odległość z miasta A do miasta B w metrach (
- kolejno odległość z miasta A do miasta B w metrach (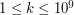 ), liczbę przejazdów kolejowych (
), liczbę przejazdów kolejowych (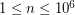 ), przyspieszenie samochodu Adama liczone w metrach na
), przyspieszenie samochodu Adama liczone w metrach na 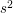 (sekundę do kwadratu) oraz ograniczenie na prędkość w metrach na sekundę (
(sekundę do kwadratu) oraz ograniczenie na prędkość w metrach na sekundę (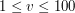 ). Kolejna linia zawiera
). Kolejna linia zawiera 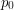 ,
, 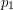 , ... ,
, ... , 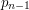 - odległości w metrach od miasta A kolejnych przejazdów kolejowych. (
- odległości w metrach od miasta A kolejnych przejazdów kolejowych. (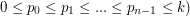 .
.

