Runda 8 [Hard] - Wypasione krowy
24.01.2011 - Damian Rusak
 
Zadanie Tygodnia Runda 8; kategoria Hard Limit czasowy: 2s; Limit pamięciowy: 32MB Wypasione krowyW dalekiej krainie, w której mieszka farmer Andrzej właśnie skończyła się zima i czas wyprowadzić krowy na pastwisko. Andrzej posiada wiele cennych gatunków krów oraz dwa piękne pastwiska porośnięte nietypowymi rodzajami trawy. Każda z krów należących do Andrzeja ma swoje własne preferencje co do chwili wypasu. Dla każdej z krów można określić dokładnie, w którym momencie może zostać wypasiona na pierwszym pastwisku i w którym można wyprowadzić ją na drugie z pastwisk. Preferencje te określa para liczb Andrzej ma swojego pomocnika, Ryszarda. On sam wyprowadza krowy na pierwsze pastwisko, Ryszard zaś na drugie. W danej chwili każdy z nich może zabrać na pastwisko dowolną liczbę krów, pod warunkiem, że każdej z nich ta chwila na tym pastwisku odpowiada (jak to było wspomniane powyżej). Ponieważ w gospodarstwie jest dużo pracy do wykonania, chcieliby aby łącznie było jak najmniej chwil w których muszą wychodzić z krowami. Znając preferencje krów, odpowiedz na pytanie, jaka jest najmniejsza liczba wyprowadzeń na wypas na obu pastwiskach, taka, aby każda z krów została wyprowadzona przynajmniej raz. Wejście: Pierwsza linia wejścia zawiera jedną liczbę Wyjście: Wyjście powinno zawierać jedną liczbę całkowitą Przykład: Wejście: 7 1 1 0 2 5 2 1 6 5 4 1 7 6 2 Wyjście: 3 Wyjaśnienie: Krowy o preferencjach
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



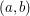 oznaczająca, że jedynym momentem odpowiednim dla danej krowy na pierwszym pastwisku jest chwila
oznaczająca, że jedynym momentem odpowiednim dla danej krowy na pierwszym pastwisku jest chwila  , zaś na drugim chwila
, zaś na drugim chwila  .
. - liczbę krów, posiadanych przez Andrzeja. W kolejnych
- liczbę krów, posiadanych przez Andrzeja. W kolejnych 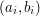 - oznaczających, że
- oznaczających, że  -ta krowa może zostać wyprowadzona na pastwisko pierwsze w chwili
-ta krowa może zostać wyprowadzona na pastwisko pierwsze w chwili 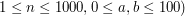 .
. - najmniejszą liczbę wyjść na pastwisko, którą w sumie muszą poczynić Andrzej i Ryszard, aby każda z krów została wyprowadzona przynajmniej raz.
- najmniejszą liczbę wyjść na pastwisko, którą w sumie muszą poczynić Andrzej i Ryszard, aby każda z krów została wyprowadzona przynajmniej raz.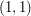 ,
, 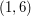 i
i 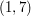 można wyprowadzić na pierwsze pastwisko w chwili
można wyprowadzić na pierwsze pastwisko w chwili  , krowy o preferencjach
, krowy o preferencjach 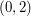 ,
, 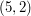 i
i 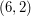 na drugie pastwisko w chwili 2, a krowę o preferencjach
na drugie pastwisko w chwili 2, a krowę o preferencjach 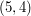 na pierwsze pastwisko w chwili 5.
na pierwsze pastwisko w chwili 5.

