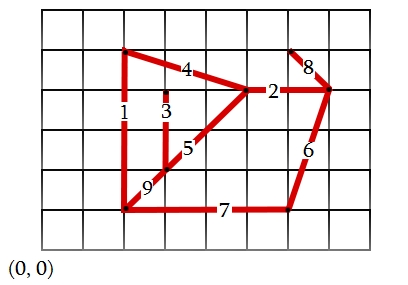
Runda 6 [Hard] - Plan twierdzy
10.01.2011 - Damian Rusak
 
Zadanie tygodnia Runda 6; kategoria Hard Limit czasowy: 2s; Limit pamięciowy: 64MB Plan twierdzyZaiste nadeszły ciężkie czasy. Nad naszym królestwem zawisła groźba inwazji nieprzyjaciela. Rozpoczęto już budowę murów obronnych, które mają chronić ludność (a przede wszystkim najważniejszych królewskich urzędników) przed wrogiem. Ty, królewski architekt, masz za zadanie czuwać nad przebiegiem prac. Tymczasem Znasz dokładnie plan budowy - wiesz, w jakiej kolejności mury zostaną ukończone i że żadne dwa nie zostaną ukończone w tym samym czasie. Odpowiedz możnym na ich pytanie - po którym zbudowanym murze będą mogli najwcześniej wszyscy schronić się w różnych bezpiecznych częściach królestwa? Wejście: Pierwsza linia wejścia zawiera liczby naturalną Wyjście: Wyjście winno składać się z jednej liczby całkowitej
Przykład 1: Wejście: 9 2 2 1 2 5 5 4 7 4 3 2 3 4 2 5 5 4 3 2 5 4 6 1 7 4 2 1 6 1 7 4 6 5 2 1 3 2 Wyjście: 9 Przykład 2: Wejście: 5 1 1 1 5 6 4 3 8 3 10 10 11 11 0 1 1 7 13 4 15 15 Wyjście: -1 Przykład 3: Wejście: 7 2 0 0 5 5 5 5 5 0 5 0 0 0 1 1 3 3 3 3 3 1 3 1 1 1 0 0 0 3 Wyjście: 6 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 najważniejszych osób w królestwie chciałoby schronić się już za murami. Nie godzą się na opuszczenie dworu króla nim wszyscy nie otrzymają bezpiecznych miejsc do przeczekania inwazji. Wszyscy na dworze króla spiskują i nienawidzą się wzajemnie. Każdy z nich postawił warunek, że ma znajdować się w innej bezpiecznej części niż reszta. Bezpieczną częścią nazwiemy każdy minimalny fragment królestwa ogrodzony murami obronnymi. (Minimalny w tym kontekście to taki, który w swoim wnętrzu nie zawiera żadnej innej bezpiecznej części - na ilustracji są to fragmenty otoczone przez mury o numerach 1,4,5,9 oraz o numerach 2,5,6,7,9).
najważniejszych osób w królestwie chciałoby schronić się już za murami. Nie godzą się na opuszczenie dworu króla nim wszyscy nie otrzymają bezpiecznych miejsc do przeczekania inwazji. Wszyscy na dworze króla spiskują i nienawidzą się wzajemnie. Każdy z nich postawił warunek, że ma znajdować się w innej bezpiecznej części niż reszta. Bezpieczną częścią nazwiemy każdy minimalny fragment królestwa ogrodzony murami obronnymi. (Minimalny w tym kontekście to taki, który w swoim wnętrzu nie zawiera żadnej innej bezpiecznej części - na ilustracji są to fragmenty otoczone przez mury o numerach 1,4,5,9 oraz o numerach 2,5,6,7,9). i
i 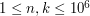 ). W kolejnych
). W kolejnych 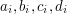 oznaczające, że
oznaczające, że  -ty fragment muru to odcinek łączący punkty
-ty fragment muru to odcinek łączący punkty 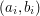
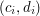
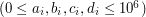 . Odcinki nie przecinają się, a jedynymi ich wspólnymi punktami mogą być ich końce.
. Odcinki nie przecinają się, a jedynymi ich wspólnymi punktami mogą być ich końce. (
(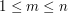 ) - najmniejszego numeru muru po którego ukończeniu istnieć będzie przynajmniej
) - najmniejszego numeru muru po którego ukończeniu istnieć będzie przynajmniej 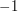 .
.