Jak patrzy na to informatyk?
Dostrzegliśmy, jak ułatwia nam zadanie nazwanie wierzchołków. Wiemy też, że skoro dopasowujemy jeden graf do drugiego, to oba muszą mieć tyle samo wierzchołków, i każdy wierzchołek pierwszego grafu łączy się z dokładnie jednym wierzchołkiem drugiego grafu. W innym razie któryś wierzchołek zostałby bez pary.
Takie przyporządkowanie każdemu z wierzchołków jednego grafu pewnego wierzchołka drugiego grafu nazywamy funkcją. Z pewnością zetknąłeś (zetknęłaś) się z tym pojęciem na lekcjach matematyki, gdzie najczęściej o funkcjach mówiło się w kontekście liczb. Funkcja jednak równie dobrze może za swoje argumenty (czyli to, co „zjada”) brać wierzchołki grafu.
Funkcja może mieć swoją nazwę. Na rysunku poniżej mamy funkcję o nazwie f. Piszemy f(1), gdy mamy na myśli wierzchołek, który został dopasowany do wierzchołka o numerze 1. Podobnie dla innych wierzchołków.
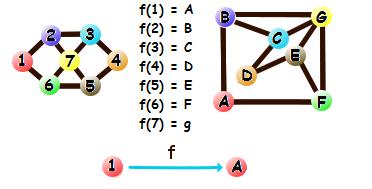
Jaki jest izomorfizm?
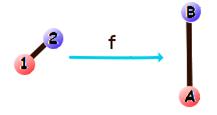
Zauważ, że ta funkcja nigdy nie przyporządkowuje dwóm różnym wierzchołkom tej samej wartości. Nie byłoby to wtedy dopasowanie, o które nam chodzi. Funkcje o takiej własności nazywamy różnowartościowymi.
Każdy wierzchołek drugiego grafu musi zostać przyporządkowany pewnemu wierzchołkowi pierwszego grafu. To oznacza, że żaden wierzchołek drugiego grafu nie zostaje bez pary. Funkcja, która ma taką własność to funkcja „na”. (Ta trochę dziwna nazwa bierze się stąd, że wykorzystaliśmy wszystkie wierzchołki drugiego grafu – funkcja jest „na” cały drugi graf).
Jeśli funkcja łączy obie powyższe własności, nazywamy ją bijekcją. Taka funkcja „działa” w obie strony (stąd przedrostek ‘bi’). Przecież równie dobrze moglibyśmy każdemu wierzchołkowi drugiego grafu przyporządkować jakiś wierzchołek pierwszego grafu, w dokładnie taki sam sposób.
W takim razie nie można tego dalej ukrywać – izomorfizm dwóch grafów z rysunku to właśnie funkcja ‘f’. Każdy izomorfizm jest w takim razie bijekcją. Dzięki temu, że myślimy o izomorfizmie jako o funkcji, możemy dokładnie opisać matematycznie nasze intuicje dotyczące podobieństwa grafów.
Podsumujmy więc, kiedy funkcja ‘f’ „z jednego grafu w drugi graf” (będziemy tak mówić, gdy mamy na myśli funkcję, która wierzchołkom pierwszego grafu przyporządkowuje wierzchołki drugiego) jest izomorfizmem:
- Gdy jest bijekcją oraz
- Gdy jeśli dla jakichkolwiek dwóch połączonych wierzchołków w pierwszym grafie (nazwijmy je A i B) wierzchołki f(A) i f(B) są połączone w drugim grafie.
Drugi warunek (o którym już była mowa wcześniej) na fragmentach naszych grafów:
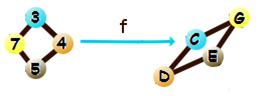
Grafy w klasach
„Bycie izomorficznym” to pewna zależność pomiędzy dwoma grafami. Takie zależności w matematyce określa się mianem relacji.
Skoro dwa izomorficzne grafy mają taką samą strukturę, to właściwie można postawić między nimi znak równości. Powiedzmy, że przyglądamy się trzem grafom o nazwach G1, G2 i G3. Jeśli G1 jest izomorficzny z G2 , a G2 jest izomorficzny z G3, to również G1 jest izomorficzny z G3. Innymi słowy, jeśli G1 jest taki sam jak G2, i G2 jest taki sam jak G3, to oczywiście G1 jest też taki sam jak G3. To oznacza, że „bycie izomorficznym” jest przechodnie.
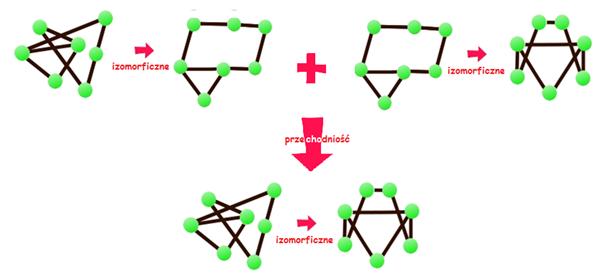
Ponadto „bycie izomorficznym” jest symetryczne. To znaczy, że jeśli G1 jest izomorficzne z G2, to również G2 jest izomorficzne z G1. Zgodziliśmy się już wcześniej, że izomorfizm „działa” w dwie strony.
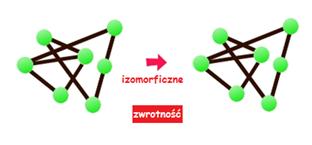
 Ponadto wiemy, że każdy graf jest izomorficzny sam ze sobą. Wbrew pozorom nie każda relacja ma tę własność (np. żadna liczba nie jest większa od samej siebie). Tę własność nazywamy zwrotnością.
Ponadto wiemy, że każdy graf jest izomorficzny sam ze sobą. Wbrew pozorom nie każda relacja ma tę własność (np. żadna liczba nie jest większa od samej siebie). Tę własność nazywamy zwrotnością.
O relacji, która jest przechodnia, symetryczna i zwrotna, mówimy że jest relacją równoważności. Oznacza to, że możemy ją traktować jak znak równości. Możemy wskazać klasy grafów takich, że każdy jest równy każdemu innemu, mając na myśli, że są takie same, izomorficzne.
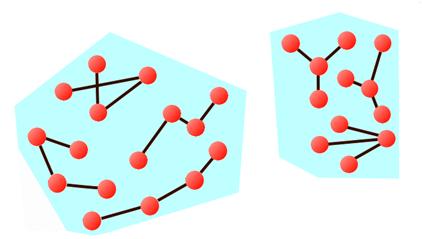
Takie zbiory izomorficznych grafów będziemy nazywać klasami równoważności, albo klasami abstrakcji. Zastanów się, czy wiele grafów należy do każdej takiej klasy?
O problemie z izomorfizmami
Wydaje się, że odpowiedź na pytanie, czy dwa grafy są izomorficzne nie jest trudna. Jednak do tej pory nie udało się znaleźć szybkiego sposobu na sprawdzenie tego dla dużych grafów. Czas działania nawet najszybszych znanych metod rośnie zdumiewająco szybko, gdy wierzchołków w grafach jest coraz więcej. Nawet, gdybyśmy mieli znacznie szybsze komputery, nie mogłyby sobie z tym problemem poradzić. Ale kto wie, może Tobie uda się kiedyś znaleźć rozwiązanie?







 Ponadto wiemy, że każdy graf jest izomorficzny sam ze sobą. Wbrew pozorom nie każda relacja ma tę własność (np. żadna liczba nie jest większa od samej siebie). Tę własność nazywamy zwrotnością.
Ponadto wiemy, że każdy graf jest izomorficzny sam ze sobą. Wbrew pozorom nie każda relacja ma tę własność (np. żadna liczba nie jest większa od samej siebie). Tę własność nazywamy zwrotnością.



