Runda 4 [Hard] - Kule śnieżne
13.12.2010 - Damian Rusak
 
Zadanie tygodnia Runda 4; kategoria Hard Limit czasowy: 1s; Limit pamięciowy: 32MB Kule śnieżneGóry i doliny pokrył śnieżny puch. Tak się właśnie złożyło, że mały Jaś wybrał się na pieszą wycieczkę na szczyt najwyższej z gór. Zauważył, że na szczycie, wzdłuż przepaści poustawiane są śnieżne kule o wszystkich możliwych rozmiarach, wyrażonych liczbami naturalnymi, od jeden włącznie. Jaś wie, że wystarczy mu sił aby zepchnąć w dół kule z pewnego przedziału - dokładnie, jeśli przypomni sobie ile kanapek zjadł rano, szybko znajdzie dwie liczby Jaś wie dobrze, że sam rozmiar niekoniecznie świadczy o tym, ile kula narobi huku w przepaści. Pamięta opowieść starego górala - jeśli weźmie się rozmiar danej kuli i policzy, ile różnych cyfr występuje w jego zapisie dziesiętnym, to taki właśnie jest współczynnik huku tej kuli. Tak więc kula rozmiaru Jaś chciałby więc policzyć, ile wynosi suma współczynników huku kul z przedziału, który uda mu się zepchnąć w przepaść. Poprosił Cię o pomoc. Wejście: Pierwsza i jedyna linia wejścia zawiera jedną liczbę całkowitą Wyjście: Dla każdego przypadku testowego należy wypisać w osobnej linii jedną liczbę całkowitą - sumę współczynników huku wszystkich kul o rozmiarach z przedziału Przykład: Wejście: 3 1 11 547892 547892 14 18 Wyjście: 12 6 10
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 i
i  ,
, 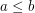 , takie, że uda mu się zepchnąć w przepaść dokładnie kule o rozmiarach
, takie, że uda mu się zepchnąć w przepaść dokładnie kule o rozmiarach 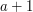 , ... ,
, ... , 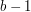 ,
, 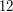 wyda bardziej imponujący dźwiękowy owoc niż kula rozmiaru
wyda bardziej imponujący dźwiękowy owoc niż kula rozmiaru 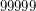 .
.  (
(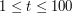 ) - liczbę przypadków testowych do rozważenia. Każdy przypadek testowy opisany jest w jednej linii przez dwie liczby
) - liczbę przypadków testowych do rozważenia. Każdy przypadek testowy opisany jest w jednej linii przez dwie liczby 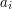
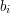 (
(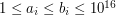 ).
).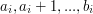 .
.

