Większość zawodników dokonała tylko jednego zgłoszenia do tego zadania, jednak większość z tych zgłoszeń okazała się niepoprawna. Ci,którym udało się rozwiązać zadanie w większości podeszli do niego jak do problemu grafowego: wyznaczali wszystkie cykle grafu oraz pozycję poszczególnych osób w tych cyklach. Po tym etapie, majacym złożoność 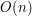 byli w stanie odpowiadać na kolejne zapytania w czasie
byli w stanie odpowiadać na kolejne zapytania w czasie 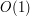 (czyli stałym). Jest to optymalne rozwiązanie tego problemu oraz podejście, którego się spodziewaliśmy.
(czyli stałym). Jest to optymalne rozwiązanie tego problemu oraz podejście, którego się spodziewaliśmy.
Tutaj przedstawimy inny sposób spojrzenia na to zadanie. Rozwiązanie będzie nieco wolniejsze - obliczenia wstępne będą miały złożoność 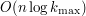 , a na pytania będziemy odpowiadali w czasie
, a na pytania będziemy odpowiadali w czasie 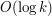 , jednak sposób rozumowania ujawni pewne ciekawe właściwości matematyczne.
, jednak sposób rozumowania ujawni pewne ciekawe właściwości matematyczne.
Na wejściu dana jest permutacja n-elementowa. Cóż to takiego? Intuicyjnie można permutację zrozumieć jako opis przekazywania sobie żarówek. Formalnie rzecz ujmując permutacja jest przyporządkowanim każdemu elementowi zbioru drugiego elementu w taki sposób, aby każdy element był przyporządkowany dokładnie jednemu. Fakt, że wejście jest permutacją był zgwarantowany przez stwierdzenie "n różnych liczb naturanych z zakresu 1 ... n". Permutację identycznościową, czyli taką, w której każdemu elementowi przyporządkowany jest on sam, zapiszemy jako
Natomiast permutację, w której każdemu elementowi przyporządkowany jest następny, a ostatniemu pierwszy (tego typu permutacja pokazana została w teście przykładowym) zapiszemy jako
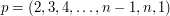 | |
Zdefiniujemy operację składania permutacji (będziemy oznaczać ją symbolem  ). Będzie ona odpowiadała uderzeniom zegara z treści zadania. W permutacji
). Będzie ona odpowiadała uderzeniom zegara z treści zadania. W permutacji  elementowi pierwszemu przyporządkowany jest drugi, a elementowi drugiemu przyporządkowany jest trzeci. Zatem po pierwszym uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru drugiego, a druga - trzeicego. Po drugim uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru trzeciego. Zatem w złożeniu permutacji
elementowi pierwszemu przyporządkowany jest drugi, a elementowi drugiemu przyporządkowany jest trzeci. Zatem po pierwszym uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru drugiego, a druga - trzeicego. Po drugim uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru trzeciego. Zatem w złożeniu permutacji  z samą sobą (co zapiszemy jako
z samą sobą (co zapiszemy jako 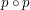 ) elementowi pierwszemu jest przyporządkowany element trzeci. Formalnie jeżeli w permutacji
) elementowi pierwszemu jest przyporządkowany element trzeci. Formalnie jeżeli w permutacji  elementowi
elementowi  jest przyporządkowany
jest przyporządkowany  , a w permutacji
, a w permutacji  elementowi
elementowi  jest przyporządkowany
jest przyporządkowany  , to w złożeniu
, to w złożeniu 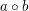 elementowi
elementowi  jest przyporządkowany
jest przyporządkowany  . Nowopowstała permutacja może zastępować nam złożenie dwóch permutacji wyjściowych w każdym wypadku (tzn. jeżeli
. Nowopowstała permutacja może zastępować nam złożenie dwóch permutacji wyjściowych w każdym wypadku (tzn. jeżeli  jest złożeniem
jest złożeniem 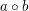 , to zawsze, gdzie pojawia się
, to zawsze, gdzie pojawia się 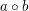 możemy napisać po prostu
możemy napisać po prostu  ).
).
Widzimy, że pytanie "jaki kolor żarówki trzyma osoba a po k uderzeniach zegara" jest równoważne pytaniu "jaki element jest przyporządkowany elementowi a w k-krotnym złożeniu permutacji z samą sobą". Wielokrotne złożenie permutacji  z samą sobą zapizsemy jako
z samą sobą zapizsemy jako 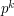 , gdzie
, gdzie  jest ilością złożeń. Obliczenie jednokrotnego złożenia permutacji ma złożoność
jest ilością złożeń. Obliczenie jednokrotnego złożenia permutacji ma złożoność 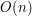 . My chcielibyśmy obliczyć złożenia
. My chcielibyśmy obliczyć złożenia 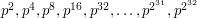 . Najpierw składamy
. Najpierw składamy 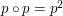 . Później możemy złożyć
. Później możemy złożyć 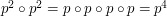 . Następnie
. Następnie 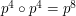 i tak dalej. Taki sposób potęgowania (nie tylko permutacji) nazywany jest szybkim potęgowaniem. Używając go każdą kolejną permutację otrzymujemy wykonując tylko jedno złożenie.
i tak dalej. Taki sposób potęgowania (nie tylko permutacji) nazywany jest szybkim potęgowaniem. Używając go każdą kolejną permutację otrzymujemy wykonując tylko jedno złożenie.
Teraz czas odpowiedzieć na zapytania. Przyjmijmy 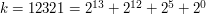 . Skorzystamy z tego, że
. Skorzystamy z tego, że
. W ten sposób rozkładamy interesującą nas permutację na złożenie permutacji, które mamy już obliczone. Teraz nie musimy składać całych permutacji - interesuje nas tylko, jaki element będzie przyporządkowany
a-temu elementowi. Zatem możemy skorzystać z definicji składania permutacji dla pojedyńczego elementu, co będzie nas to kosztowało zaledwie
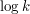
(każda wartość
k rozkłada się na conajwyżej
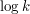
potęg dwójki).
Zastanów się, czy istnieje taka wartość  , że
, że 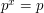 ? Jeżeli umiemy składać permutacje, jak wykonać działanie odwrotne?
? Jeżeli umiemy składać permutacje, jak wykonać działanie odwrotne?
Wiktor Janas

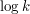 (każda wartość k rozkłada się na conajwyżej
(każda wartość k rozkłada się na conajwyżej 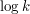 potęg dwójki).
potęg dwójki).


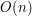 byli w stanie odpowiadać na kolejne zapytania w czasie
byli w stanie odpowiadać na kolejne zapytania w czasie 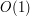 (czyli stałym). Jest to optymalne rozwiązanie tego problemu oraz podejście, którego się spodziewaliśmy.
(czyli stałym). Jest to optymalne rozwiązanie tego problemu oraz podejście, którego się spodziewaliśmy.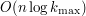 , a na pytania będziemy odpowiadali w czasie
, a na pytania będziemy odpowiadali w czasie 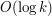 , jednak sposób rozumowania ujawni pewne ciekawe właściwości matematyczne.
, jednak sposób rozumowania ujawni pewne ciekawe właściwości matematyczne.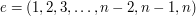
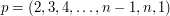
 ). Będzie ona odpowiadała uderzeniom zegara z treści zadania. W permutacji
). Będzie ona odpowiadała uderzeniom zegara z treści zadania. W permutacji  elementowi pierwszemu przyporządkowany jest drugi, a elementowi drugiemu przyporządkowany jest trzeci. Zatem po pierwszym uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru drugiego, a druga - trzeicego. Po drugim uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru trzeciego. Zatem w złożeniu permutacji
elementowi pierwszemu przyporządkowany jest drugi, a elementowi drugiemu przyporządkowany jest trzeci. Zatem po pierwszym uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru drugiego, a druga - trzeicego. Po drugim uderzeniu zegara osoba pierwsza będzie trzymała żarówkę koloru trzeciego. Zatem w złożeniu permutacji 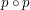 ) elementowi pierwszemu jest przyporządkowany element trzeci. Formalnie jeżeli w permutacji
) elementowi pierwszemu jest przyporządkowany element trzeci. Formalnie jeżeli w permutacji  elementowi
elementowi  jest przyporządkowany
jest przyporządkowany  , a w permutacji
, a w permutacji  elementowi
elementowi  , to w złożeniu
, to w złożeniu 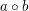 elementowi
elementowi  jest złożeniem
jest złożeniem 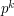 , gdzie
, gdzie  jest ilością złożeń. Obliczenie jednokrotnego złożenia permutacji ma złożoność
jest ilością złożeń. Obliczenie jednokrotnego złożenia permutacji ma złożoność 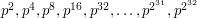 . Najpierw składamy
. Najpierw składamy 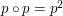 . Później możemy złożyć
. Później możemy złożyć 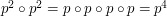 . Następnie
. Następnie 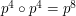 i tak dalej. Taki sposób potęgowania (nie tylko permutacji) nazywany jest szybkim potęgowaniem. Używając go każdą kolejną permutację otrzymujemy wykonując tylko jedno złożenie.
i tak dalej. Taki sposób potęgowania (nie tylko permutacji) nazywany jest szybkim potęgowaniem. Używając go każdą kolejną permutację otrzymujemy wykonując tylko jedno złożenie.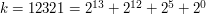 . Skorzystamy z tego, że
. Skorzystamy z tego, że 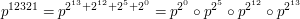
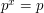 ? Jeżeli umiemy składać permutacje, jak wykonać działanie odwrotne?
? Jeżeli umiemy składać permutacje, jak wykonać działanie odwrotne?

