"normalne"
Powiedzieliśmy, że jasność obiektu zależy od kąta padania promieni światła na jego powierzchnię.
Będziemy zatem potrzebować informacji o orientacji tej powierzchni w przestrzeni. Możemy ją uzyskać stosując
tzw. wektor normalny. Jest to wektor o długości równej jeden, ortogonalny do powierzchni z którą jest związany.
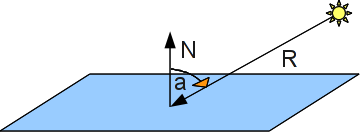
Rys. 6 Kąt pomiędzy płaszczyzną i promieniem.
N - normalna płaszczyzny
R - promień ze źródła światła do punktu w którym liczone jest natężenie światła.
Niestety Open GL nie jest w stanie obliczyć za nas normalnych dla podstawowych figur geometrycznych.
Na szczęście, dla naszego sześcianu, bardzo łatwo znajdziemy wektory normalne, gdyż jego ściany są do osi układu współrzędnych prostopadłe.
Aby wprowadzić normalne do naszego kodu, powinniśmy zmienić definicję klasy vertex3f i dodać klasę odpowiedzialną za przechowywanie współrzędnych
wektorów. Najpierw dodamy strukturę reprezentującą wektor.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| /**
* @struct vector3f
* @brief Struktura przechowująca współrzędne wektora
*/
struct vector3f
{
/**
* @brief Domyslny konstruktor
* Ustawia wszystkie wspolrzedne na ( 0, 0, 0 )
*/
vector3f( void ) : x( .0f ), y( .0f ), z( .0f )
{
}
/**
* @brief Konstruktor ustawiajacy wspolrzedne
* @param in_x wspolrzedna x
* @param in_y wspolrzedna y
* @param in_z wspolrzedna z
*/
vector3f( GLfloat in_x, GLfloat in_y, GLfloat in_z )
: x( in_x ), y( in_y ), z( in_z )
{
}
///wspolrzedna x
GLfloat x;
///wspolrzedna y
GLfloat y;
///wspolrzedna z
GLfloat z;
}; |
Następnie modyfikujemy strukturę vertex3f tak aby uwzględniała użycie nowego typu danych i podziału na pozycję wierzchołka oraz jego normalną.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| /**
* @struct vertex3f
* @brief Struktura opisujaca wierzchołek w przestrzeni 3d
*/
struct vertex3f
{
typedef vector3f position_type;
typedef vector3f normal_type;
/**
* @brief Domyslny konstruktor
* Ustawia wszystkie wektory na ( 0, 0, 0 )
*/
vertex3f( void ) { }
/**
* @brief Konstruktor ustawiajacy wspolrzedne
* @param pos pozycja wierzchołka w przestrzeni
* @param n normalna wierzcholka
*/
explicit vertex3f( const position_type& pos,
const normal_type& n )
: position( pos ), normal( n )
{
}
///pozycja wierzchołka
position_type position;
///normalna w wierzchołku
normal_type normal;
}; |
Musimy jeszcze podać odpowiednie wartości wektorów normalnych, podczas tworzenia tablicy wierzchołków.
Zmodyfikujmy zatem funkcję createCube.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| //początek bez zmian
.
.
.
//przednia sciana
ret.push_back(
vertex3f( vector3f( min, max, max ),
vector3f( .0f, .0f, 1.0f ) ) );
ret.push_back(
vertex3f( vector3f( min, min, max ),
vector3f( .0f, .0f, 1.0f ) ) );
ret.push_back(
vertex3f( vector3f( max, min, max ),
vector3f( .0f, .0f, 1.0f ) ) );
ret.push_back(
vertex3f( vector3f( max, max, max ),
vector3f( .0f, .0f, 1.0f ) ) );
//dalsze zmiany analogicznie
.
.
. |
Po tych wszystkich zmianach biblioteka Open GL zna wszystkie dane potrzebne do poprawnego wyliczenia jasności oraz koloru obiektów, na które wpływa światło.







