Ewolucja węża
31.08.2011 - Tomasz Urbański i Tomasz Kupczyk
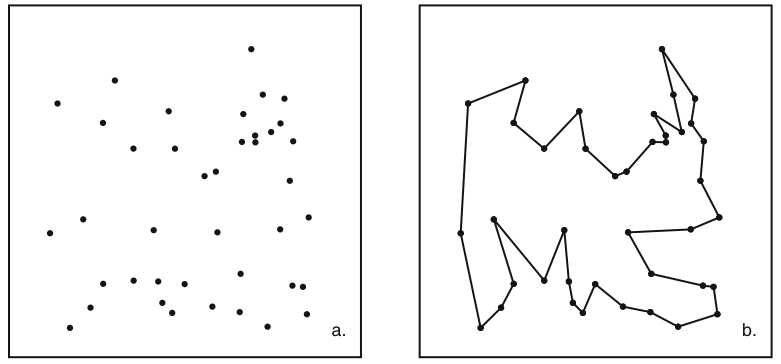
  DLACZEGO WYBRALIŚMY TAKĄ DROGĘ ? Opisany problem możemy rozwiązać na wiele sposobów. Gdyby jednak na planszy dodatkowo umieścić przeszkody problem stałby się o wiele bardziej złożony. Wybór algorytmów ewolucyjnych nie jest zatem przypadkowy. Napotykając na jakiś problem zaczynamy go analizować, aby znaleźć jego rozwiązanie. Jednak czasami zdarzają się problemy, dla których znalezienie rozwiązania trwałoby wieki. Nie jest to rezultatem nieudolnego poszukiwania rozwiązania problemu, lecz wynika z jego natury. Przykładem takiego trudnego zagadnienia jest problem komiwojażera. W uproszczeniu, problem ten polega na znalezieniu takiej trasy pomiędzy miejscowościami, która rozpoczyna się i kończy w tej samej miejscowości,a dodatkowo jest najkrótsza. Przykładowe rozwiązanie tego problemu znajduje się na rysunku poniżej.
Ten problem należy do klasy problemów NP-trudnych. Napotykając na problemy z tej klasy unikajmy poszukiwania metod dokładnego ich rozwiązania. Bywają również problemy, które nie są NP-trudne, ale są na tyle złożone, że również nie rozwiążemy ich w akceptowalnym czasie. Co wtedy ? Wtedy używamy algorytmów które znajdą nam rozwiązanie przybliżone. Oczywiście będzie one gorsze od optymalnego. Algorytmy ewolucyjne to jedne z wielu rodzajów algorytmów które służą do poszukiwania rozwiązań przybliżonych OŻYWIĆ WĘŻA W pierwotnej wersji gry Snake to człowiek kieruje ruchami węża, można jednak stworzyć mechanizm dzięki któremu wąż zacznie w końcu sam decydować o swoim losie. By umożliwić wężowi samodzielne poruszanie się posłużmy się powszechnie stosowaną strukturą danych, drzewem. Za pomocą drzewa można wyznaczyć kolejny ruch węża w zależności od stanu gry (Rys. 2).
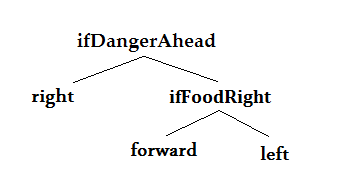
W węzłach drzewa znajdują się różne warunki, natomiast w liściach ruchy jakie może wykonać wąż. Przeanalizujmy drzewo decyzji z Rys. 2 w kontekście przykładowego stanu gry przedstawionego na pierwszym rysunku poniżej (Rys. 3), by lepiej zrozumieć jak zachowa się wąż w danej sytuacji.
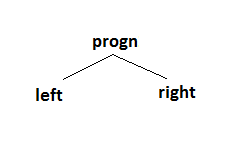
Jak widać na rysunku wąż porusza się do góry i ma jedzenie po swojej lewej stronie. Zacznijmy odczytywać drzewo od korzenia, w którym znajduje się warunek ifDangerAhead . Warunek ten jest prawdziwy, gdy w następnym ruchu bez zmiany aktualnego kierunku ruchu, wąż uderzyłby w ścianę, lub ugryzł siebie. W zaprezentowanym przykładowym stanie gry niebezpieczeństwa takiego nie ma, więc warunek jest fałszywy. W takiej sytuacji kontynuujemy procedurę dla prawego poddrzewa. W kolejnym węźle znajduje się warunek ifFoodRight. W zaprezentowanej na Rys.3 sytuacji, warunek ten jest fałszywy, ponieważ jedzenie znajduje się na lewo od głowy węża, więc postępujemy dalej według procedury dla prawego poddrzewa. Napotykamy liść decyzyjny left więc wąż skręci w lewo. Środkowy rysunek obrazuje nowy stan gry po skręcie węża w lewo. Rysunek od prawej to stan gry po wykonaniu omawianego drzewa decyzji na nowym stanie. Oczywiście w drzewie decyzji mogą znajdować się również inne warunki. Poniżej znajduje się opis kilku możliwych warunków wraz z opisem: ifFoodRight – jedzenie znajduje się na prawo od węża, ifDangerRight – w polu na prawo od głowy węża znajduje się ściana lub jego ciało, ifDangerTwoAhead – w którymś z dwóch pól naprzeciwko węża , znajduje się ściana lub jego ciało, ifMovingRight – wąż porusza się w prawo. Istnieje również specjalna komenda która może pojawić się w węźle drzewa, a mianowicie progn. Komenda ta sprawia, że w aktualnej turze wąż wykona ruch zgodny z logiką lewego poddrzewa, a w następnej turze tak jak to będzie wynikało z obliczeń dla prawego poddrzewa. Na Rys.4 znajduje się przykładowe drzewo decyzji zawierające komendę progn.
Zacznijmy odczytywać drzewo od korzenia. Znajduje się w nim komenda progn, więc teraz kontynuujemy procedurę dla lewego poddrzewa. Znajduje się tam liść left, więc wąż skręci w lewo. Aby wyznaczyć kolejny ruch węża, nie zaczniemy analizować od korzenia drzewo decyzji, gdyż wcześniej napotkaliśmy omawianą komendę. Tym samym następny ruch węża będzie wyznaczony na podstawie prawego poddrzewa węzła w którym znajduje się progn. Ponieważ w prawym poddrzewie znajduje się jedynie liść right to w kolejnym ruchu wąż skręci w prawo.Dwa kolejne ruchy wykonane przez węża zostały zilustrowane na rysunku nr 5.
Oczywiście komenda progn może występować wielokrotnie w drzewie decyzji. Za pomocą tych warunków można stworzyć bardzo rozbudowane drzewa decyzji. Teraz zastanówmy się jak modyfikować drzewa. (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com