Bezbolesne wprowadzenie do MapReduce
16.12.2009 - Paweł Ledwoń
  Ostatni przykładSzacowanie liczby πOstatnim – i najciekawszym – rozważanym w tym artykule problemem jest szacowanie liczby π. Problem w obliczaniu wartości π jest związany z faktem, że jest ona liczbą niewymierną – nie da się jej przedstawić w postaci ułamka prostego. Możemy co najwyżej poszukać ułamka, który będzie ją wystarczająco dobrze przybliżał. Do szacowania wykorzystamy metodę Monte Carlo obliczania pola powierzchni koła. Zauważmy bowiem, że pole powierzchni koła O o promieniu r = 1 wynosi:
Jeżeli środek koła umieścimy w punkcie (0, 0), to będzie ono w całości zawarte w kwadracie K o polu SK = 4, wyznaczonym przez proste x = -1, x = 1, y = -1 i y = 1. Załóżmy, że chcemy znaleźć przybliżenie π przez liczbę
a =
Rozwiązanie naszego problemu sprowadza się więc do obliczenia ilości punktów z przestrzeni [-1; 1]2 należących do koła o środku (0, 0) i promieniu jednostkowym. Podzielmy kwadrat K na siatkę m2 równych
kwadratów o długości boku Funkcja map otrzymuje jako argumenty współrzędne opisujące kwadrat K', w którym ma losować punkty – na przykład indeks wiersza i kolumny, na przecięciu których leży dany kwadrat. Generowane jest p punktów należących do K'. Wartością funkcji jest liczba p' oznaczająca liczbę punktów, które należą do O. Liczby powinny być przekazywane jako wartość z ustalonym wcześniej stałym kluczem, żeby możliwe było ich zgrupowanie i przekazanie wszystkich do jednego wywołania reduce. Funkcja reduce sumuje wszystkie wartości zwrócone przez wywołania map, ich sumę dzieli przez iloczyn pM i mnoży razy 4 (pole powierzchni kwadratu K). Otrzymana liczba jest przybliżeniem pola koła O, czyli szukaną przez nas liczbą π. Powyższy opis implikuje, że liczba R zadań reduce będzie równa 1. Ponadto, funkcja reduce zostanie wywołana tylko raz, gdyż wszystkie wartości obliczone w pierwszej fazie zostaną zgrupowane względem identycznego klucza. Wynik jedynego wywołania reduce – czyli przybliżenie π – zostanie zapisany w jedynym pliku wyjściowym. Skuteczność opisanej metody jest wysoce zależna od jakości generatora liczb losowych. Zachwiany rozkład punktów może wypaczyć jakość przybliżenia. Należy z rozwagą dobierać generator i liczbę losowanych punktów, gdyż generatory po pewnym czasie wpadają w cykl i zwracają ponownie te same liczby, co wpływa na wynik raczej negatywnie. PodsumowanieGoogle wywołało spore zainteresowanie udostępniając wyniki swoich badań nad MapReduce, lecz od tamtego czasu pojawiło się niewiele nowych informacji na temat omawianego systemu. Nie znamy (niestety) zbyt wielu szczegółów wewnętrznej implementacji frameworka Google. Jednak liczby mówią same za siebie – 20 petabajtów danych dziennie przetwarzanych przy pomocy MapReduce przez Google czy sortowanie 10 bilionów 100-bajtowych kluczy (1PB danych) w około 6 godzin – to tylko jedne z nich. Takie statystyki niewątpliwie pokazują, jak wiele pracy zostało włożone w implementację MapReduce. Nie dało się uniknąć kilku negatywnych opinii na temat skuteczności systemu – zarzucano mu głównie mało innowacyjny model obliczeniowy i ograniczenia przez niego narzucone. Nie każdy problem da się dobrze rozwiązać z pomocą MapReduce, jednak istnieją dziedziny, w których system jest bezkonkurencyjny i nie zapowiada się, żeby szybko sytuacja ta miała ulec zmianie. HadoopMimo tego, że implementacja autorstwa Google jest pilnie strzeżona przez firmę, istnieją inne systemy pozwalające na korzystanie z dobrodziejstw MapReduce. Najpopularniejszym systemem jest Hadoop, w którego skład wchodzą dodatkowo rozproszony system plików HDFS (odpowiednik Google File System) i kolumnowa baza danych HBase (wzorowana na Google BigTable), elementy niemalże niezbędne do pracowania z MapReduce.
System został zaimplementowany w języku Java, lecz istnieje możliwość połączenia go z dowolnym innym językiem (przez Hadoop Streaming). Oczywiście nie trzeba posiadać klastra komputerów, żeby uruchomić swoją aplikację MapReduce – istnieje możliwość działania w środowisku pseudo-rozproszonym, symulowanym w całości na jednym komputerze. Wydajność Hadoopa stoi na wysokim poziomie, o czym świadczą dwa zwycięstwa w benchmarku TeraSort 2009, kategorii Daytona. Osobiście polecam eksperymentowanie z systemem jako szansę na zapoznanie się z modelem MapReduce przy stosunkowo niewielkim nakładzie pracy własnej. (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


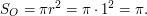
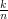 . Wylosujmy n punktów należących do kwadratu
K. Stosunek powierzchni koła O do powierzchni kwadratu
K możemy przybliżyć jako iloraz
. Wylosujmy n punktów należących do kwadratu
K. Stosunek powierzchni koła O do powierzchni kwadratu
K możemy przybliżyć jako iloraz 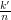 , gdzie k' to
liczba wylosowanych punktów, które są zawarte w O. Zatem:
, gdzie k' to
liczba wylosowanych punktów, które są zawarte w O. Zatem:
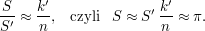
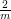 . Każdemu z nich będzie odpowiadało
jedne zadanie map, więc w tym przypadku M = m2.
Przyjmijmy z góry liczbę punktów p, które będziemy losować w jednym z
mniejszych kwadratów.
. Każdemu z nich będzie odpowiadało
jedne zadanie map, więc w tym przypadku M = m2.
Przyjmijmy z góry liczbę punktów p, które będziemy losować w jednym z
mniejszych kwadratów.



