|
|
Własny silnik graficzny. Część I: podstawy śledzenia promieni.
30.11.2010 - Robert Kraus
Teraz przejdziemy do implementacji.
Kilka stałych globalnych
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| std::numeric_limits<float> real;
const float epsilon3 = 0.001f; // stała dla błędów zaokrągleń numerycznych
const float epsilon5 = 0.00001f; // stała dla błędów zaokrągleń numerycznych
const float infinity = real.infinity(); // nieskończoność
const float undefined = real.infinity(); // wartość niezdefiniowana
const float Pi = 3.14159265f;
const float PiMul2 = 6.28318530f;
typedef unsigned int nat; // typ liczb naturalnych
#define nt(x) ((nat)(x)) // rzutowanie na liczby naturalne
#define fl(x) ((float)(x)) // rzutowanie na liczby rzeczywiste
#define bt(x) ((unsigned char)(x)) // rzutowanie na liczby {0..255}
#define isNull(ptr) ( NULL == ptr ) // czy wskaźnik jest pusty
#define notNull(ptr) ( NULL != ptr ) // czy wskaźnik jest niepusty
// liczba losowa z przedziału [0,1] (rozkład jednostajny)
inline float uRand() { return fl(rand()) / fl(RAND_MAX); } |
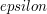 jest stałą dla błędów wynikających z zaokrągleń numerycznych.
Liczby zmiennoprzecinkowe mają niestety ograniczoną precyzję,
dlatego wyników działań na takich liczbach nie powinniśmy porównywać używając
bezpośredino operacji takich jak jest stałą dla błędów wynikających z zaokrągleń numerycznych.
Liczby zmiennoprzecinkowe mają niestety ograniczoną precyzję,
dlatego wyników działań na takich liczbach nie powinniśmy porównywać używając
bezpośredino operacji takich jak 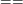 , , 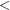 , , 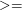 . Przykładowo, aby uniknąć
niepożądanych zjawisk, zwykle lepiej wykonać porównanie . Przykładowo, aby uniknąć
niepożądanych zjawisk, zwykle lepiej wykonać porównanie 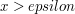 zamiast zamiast 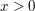 ,
bądź też uznać, że ,
bądź też uznać, że  jest równy zeru wtedy, gdy zachodzi jest równy zeru wtedy, gdy zachodzi 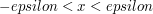 . .
Czasami wynikiem jakiegoś działania będzie nieskończoność, stąd przyda nam sie stała 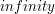 ,
i czasem będziemy sprawdzać czy pewna odległość jest mniejsza od nieskończoności.
Dodatkowo przyda się alias ,
i czasem będziemy sprawdzać czy pewna odległość jest mniejsza od nieskończoności.
Dodatkowo przyda się alias 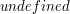 dla nieskończoności, którego będziemy używać do tego,
aby jawnie określać coś jako niezdefiniowane, co jednak może się zdefiniować w wyniku obliczeń,
które będą wykonywały zapytanie postaci dla nieskończoności, którego będziemy używać do tego,
aby jawnie określać coś jako niezdefiniowane, co jednak może się zdefiniować w wyniku obliczeń,
które będą wykonywały zapytanie postaci 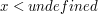 (jeśli (jeśli  nie jest nieskończonością,
odpowiedzią na takie zapytanie powinno być zdanie: "tak, nie jest nieskończonością,
odpowiedzią na takie zapytanie powinno być zdanie: "tak,  jest mniejszy"). jest mniejszy").
Podstawowe definicje wektorowe
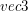 to element przestrzeni trójwymiarowej, czasami będzie symbolizował punkt, a czasami wektor,
stąd czwarty argument w jednym z konstruktorów tej struktury narzucający długość wektora. to element przestrzeni trójwymiarowej, czasami będzie symbolizował punkt, a czasami wektor,
stąd czwarty argument w jednym z konstruktorów tej struktury narzucający długość wektora.
1
2
3
4
5
6
7
8
9
10
11
12
13
| struct vec3 {
typedef const vec3& i; // input ref
typedef vec3& io; // input/output ref
float x, y, z;
vec3() { x = y = z = 0.0f; }
vec3(float x2, float y2, float z2) : x(x2), y(y2), z(z2) {}
vec3(float x2, float y2, float z2, float len) : x(x2), y(y2), z(z2) {
float newLen = len / sqrt(x*x + y*y + z*z);
x *= newLen; y *= newLen; z *= newLen;
}
}; |
Poniżej elementarne operacje arytmetyczne dla wektorów.
Pokaż/ukryj kod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| inline vec3 operator+ (vec3::i a, vec3::i b)
{ return vec3(a.x+b.x, a.y+b.y, a.z+b.z); }
inline void operator+= (vec3::io a, vec3::i b)
{ a = a + b; }
inline vec3 operator- (vec3::i a, vec3::i b)
{ return vec3(a.x-b.x, a.y-b.y, a.z-b.z); }
inline void operator-= (vec3::io a, vec3::i b)
{ a = a - b; }
inline vec3 operator* (vec3::i a, float t)
{ return vec3(a.x*t, a.y*t, a.z*t); }
inline vec3 operator/ (vec3::i a, float t)
{ return vec3(a.x/t, a.y/t, a.z/t); } |
Pozostałe operacje wektorowe.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| // przekształcenie wektora u na wektor -u
inline vec3 invert(vec3::i u)
{ return vec3(-u.x,-u.y,-u.z); }
// przekształcenie wektora u na wektor o długości 1
inline vec3 unitise(vec3::i u)
{ return vec3(u.x, u.y, u.z, 1.0f); }
// długość wektora 3d
inline float length(vec3::i v)
{ return sqrt(v.x*v.x + v.y*v.y + v.z*v.z); }
// odległość pomiędzy punktami p1 i p2
inline float distance(vec3::i p1, vec3::i p2)
{ return length(p2 - p1); }
// iloczyn skalarny wektorów v1 i v2
inline float dotProd(vec3::i v1, vec3::i v2)
{ return v1.x*v2.x + v1.y*v2.y + v1.z*v2.z; }
// iloczyn wektorowy wektorów v1 i v2
// wynikiem jest wektor prostopadły do wektorów v1 i v2
inline vec3 uCrossProd(vec3::i v1, vec3::i v2) {
return vec3(
v1.y*v2.z - v2.y*v1.z,
v1.z*v2.x - v2.z*v1.x,
v1.x*v2.y - v2.x*v1.y,
1.0f
);
}
// przeniesienie wektora V do przestrzeni zbudowanej na wektorach Ex, Ey, Ez
// oraz jego normalizacja
inline vec3 uChangeSpace(vec3::i V, vec3::i Ex, vec3::i Ey, vec3::i Ez) {
return vec3(
V.x*Ex.x + V.y*Ey.x + V.z*Ez.x,
V.x*Ex.y + V.y*Ey.y + V.z*Ez.y,
V.x*Ex.z + V.y*Ey.z + V.z*Ez.z,
1.0f
);
} |
Promień światła
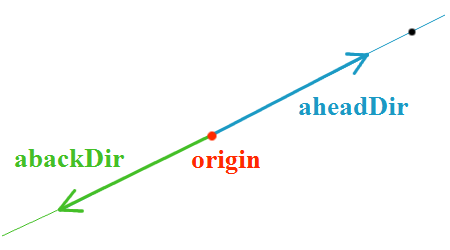
Promień światła definiujemy przy pomocy punktu, z którego został wystrzelony, czyli jego źródła (ang. 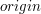 )
oraz z pary wektorów )
oraz z pary wektorów 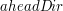 i i 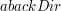 .
Oba wektory mają ten sam kierunek, ale przeciwne zwroty (tj. .
Oba wektory mają ten sam kierunek, ale przeciwne zwroty (tj. 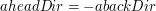 ). ).
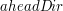 jest wektorem o zwrocie wskazującym kierunek poruszania się promienia. jest wektorem o zwrocie wskazującym kierunek poruszania się promienia.
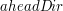 będzie przydatny podczas szukania najbliższego obiektu, w który uderza promień,
natomiast będzie przydatny podczas szukania najbliższego obiektu, w który uderza promień,
natomiast 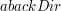 będzie przydatny w obliczeniach związanych z obliczaniem odbić, załamań jak i natężenia światła. będzie przydatny w obliczeniach związanych z obliczaniem odbić, załamań jak i natężenia światła.
1
2
3
4
5
6
7
8
9
| struct ray {
typedef const ray& i; // input ref
vec3 origin;
vec3 abackDir;
vec3 aheadDir;
ray(vec3 origin, vec3 aheadDir2) :
origin(origin), aheadDir(aheadDir2), abackDir(invert(aheadDir2)) {}
}; |
Kolor i charakterystyka materiału
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| // przycinanie wartości ujemnych do zera (typ float)
#define CUT(x) ( x < 0.0f ? 0.0f : x )
struct color {
typedef const color& i; // input ref
typedef color& io; // input/output ref
float r, g, b;
color() { r = g = b = 0.0f; }
color(float r, float g, float b) : r(r), g(g), b(b) {}
color(float v) { r = g = b = CUT(v); }
};
color // kolory:
black(0.0f), // czarny
grey(0.9f), // szary
white(1.0f), // biały
red(0.95f, 0.32f, 0.23f), // czerwony
green(0.71f, 0.89f, 0.1f), // zielony
blue(0.19f, 0.77f, 0.98f), // niebieski
darkBlue(0.04f, 0.42f, 0.5f), // ciemny niebieski
yellow(1.0f, 0.98f, 0.74f); // żółty |
Kolor definiujemy jako trójkę liczb z przedziału 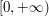 .
Dlaczego nie jest to trójka liczb z przedziału .
Dlaczego nie jest to trójka liczb z przedziału ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) ?
Tutaj kolor jest synonimem energii, która jest nieujemna i może być dowolnie duża.
Dopiero chcąc przekształcić tą energię na kolor piksela będziemy musieli konwertować
nasz kolor do liczb z przedziału ?
Tutaj kolor jest synonimem energii, która jest nieujemna i może być dowolnie duża.
Dopiero chcąc przekształcić tą energię na kolor piksela będziemy musieli konwertować
nasz kolor do liczb z przedziału ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) . Najprostszym rozwiązainem
(niekoniecznie najlepszym, ale często zadowalającym)
jest obcinanie do jedynki wartości większych od jedynki.
Poniżej operacje jakie będziemy potrzebowali wykonywać na kolorach. . Najprostszym rozwiązainem
(niekoniecznie najlepszym, ale często zadowalającym)
jest obcinanie do jedynki wartości większych od jedynki.
Poniżej operacje jakie będziemy potrzebowali wykonywać na kolorach.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| // sprawdzanie czy kolor ma przynajmniej jeden niezerowy kanał
inline bool isBlack(color::i c)
{ return (c.r + c.g + c.b > 0.0f) ? false : true; }
///// operacje arytmetyczne dla kolorów
inline color operator+ (color::i a, color::i b)
{ return color(a.r + b.r, a.g + b.g, a.b + b.b); }
inline void operator+= (color::io a, color::i b)
{ a = a + b; }
inline color operator- (color::i a, color::i b)
{ return color(a.r - b.r, a.g - b.g, a.b - b.b); }
inline color operator* (color::i a, color::i b)
{ return color(a.r * b.r, a.g * b.g, a.b * b.b); }
inline color operator* (color::i a, float t)
{ return color(a.r * t, a.g * t, a.b * t); }
inline color operator/ (color::i a, float c)
{ return color(a.r / c, a.g / c, a.b / c); } |
Materiał opisuje ile światła i o jakim kolorze odbije się od powierzchni lub zostanie przepuszczone przez powierzchnię.
Sensownie jest założyć, że powierzchnia nie odbija i nie przepuszcza więcej światła niż tyle, ile do niej przychodzi,
zatem dla każdego z kanałów R, G, B powinna zachodzić własność:
![$ dr*cMap[i] $](/files/tex/4089c9a58322d2ac58e1f2f85eaf114a731d0cca.png) + + 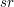 + + 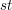 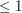 , gdzie , gdzie  jest indeksem dowolnego teksela tekstury. jest indeksem dowolnego teksela tekstury.
W przypadku materiału kolory nie oznaczają energii, a jedynie odbijalność i przepuszczalność,
dlatego wszystkie składowe kolorów powinny należeć do przedziału ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) . .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| struct material {
color dr; // diffuse reflectance (odbicie rozproszone)
colorMap* drMap; // diffuse reflectance map
color sr; // specular reflectance (odbicie zwierciadlane)
color st; // specular transmittance (transmisja zwierciadlana)
float ior; // index of refraction (indeks refrakcji)
vectorMap* normalMap; // mapa wektorów normalnych
bool isDiffuse; // czy materiał odbija z rozproszeniem
bool isSpecular; // czy materiał odbija zwierciadlanie
bool isTransmittive; // czy materiał transmituje
bool hasTextures; // czy materiał posiada tekstury
bool hasDrMap; // czy materiał posiada mapę odbicia rozproszonego
bool hasNormalMap; // czy materiał posiada mapę wektorów normalnych
// konstruktory
};
material
pureGlass(black, black, white, 1.4f), // szkło
darkBlueGlass(darkBlue, darkBlue), // ciemno-niebiesko szkło
redStone(red, black), // czerwony kamień
greenStone(green, black), // zielony kamień
blueStone(blue, black), // niebieski kamień
yellowStone(yellow, black); // żółty kamień |
Źródło światła i obliczanie oświetlenia
Posłużymy się prostym rodzajem źródła światła (które nie ma fizycznego sensu,
ale jest łatwe w obsłudze)  światłem punktowym. Zakładamy, że światło takie jest punktem
emitującym światło tak samo intensywne we wszystkich kierunkach. Natężenie światła reprezentujemy
jako kolor o składowych z przedziału światłem punktowym. Zakładamy, że światło takie jest punktem
emitującym światło tak samo intensywne we wszystkich kierunkach. Natężenie światła reprezentujemy
jako kolor o składowych z przedziału 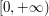 . Oprócz natężenia, które będzie odgrywało rolę
w bezpośrednim oświetleniu dajemy źródłu światła jeszcze jedną cechę - wkład w światło tła.
Jeżeli w pokoju jedynym źródłem światła jest lampa umieszczona przy suficie,
to światło z lampy nie dociera bezpośrednio np. pod stolik umieszczony w pokoju.
Wydawałoby się więc, że pod stolikiem powinna być całkowita ciemność,
a jednak tak nie jest. Dzieje się tak dlatego, że światło odbija się od innych obiektów
wpadając w przestrzeń pod stołem. Nie jest to łatwe do symulowania w sposób dokładny,
jednak można dokonać pewnego uproszczenia - założyć, że światło tła pochodzące ze
źródła światła jest stałe w całej scenie i doświetlić nim wszystkie obiekty sceny.
Dzięki temu w miejscach, gdzie światło nie dociera bezpośrednio,
nie będziemy mieli pełnych cieni w postaci czarnych plam. . Oprócz natężenia, które będzie odgrywało rolę
w bezpośrednim oświetleniu dajemy źródłu światła jeszcze jedną cechę - wkład w światło tła.
Jeżeli w pokoju jedynym źródłem światła jest lampa umieszczona przy suficie,
to światło z lampy nie dociera bezpośrednio np. pod stolik umieszczony w pokoju.
Wydawałoby się więc, że pod stolikiem powinna być całkowita ciemność,
a jednak tak nie jest. Dzieje się tak dlatego, że światło odbija się od innych obiektów
wpadając w przestrzeń pod stołem. Nie jest to łatwe do symulowania w sposób dokładny,
jednak można dokonać pewnego uproszczenia - założyć, że światło tła pochodzące ze
źródła światła jest stałe w całej scenie i doświetlić nim wszystkie obiekty sceny.
Dzięki temu w miejscach, gdzie światło nie dociera bezpośrednio,
nie będziemy mieli pełnych cieni w postaci czarnych plam.
1
2
3
4
5
6
7
8
| struct lightSrc {
vec3 location; // położenie światła
color intensity; // natężenie światła
color ambient; // wkład w światło tła
lightSrc(vec3 location, color intensity) :
location(location), intensity(intensity), ambient(intensity / 4.0f) {}
}; |
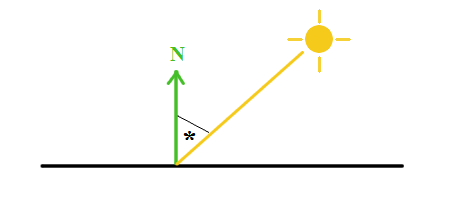
Funkcja 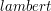 oblicza natężenie światła padające ze źródła światła na punkt oblicza natężenie światła padające ze źródła światła na punkt 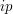 . .
W wierszu nr 11 sprawdzamy, czy obiekt, z którym zderzył się promień cienia, znajduje się przed
źródłem światła. Jeśli tak, to nasz obiekt jest w cieniu i zwracamy kolor światła tła.
W przeciwnym wypadku dajemy w wyniku intensywność bazową źródła światła przeskalowaną
cosinusem kąta  (z ilustracji) plus światło tła. Im wiekszy kąt padania światła, tym mniejsza jest intensywność światła padającego na punkt (z ilustracji) plus światło tła. Im wiekszy kąt padania światła, tym mniejsza jest intensywność światła padającego na punkt  . .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| // n - wektor normalny do powierzchni w punkcie ip
// ip - punkt przecięcia powierzchni z promieniem
// s - scena
inline color lambert(hit& h, scene& s) {
vec3 toLightDir = unitise(s.light.location - h.ip); // kierunak do światła
float cosNL = dotProd(h.N, toLightDir); // cos kąta pomiędzy N i toLightDir
if (cosNL < 0.0f) return s.light.ambient; // światło pada pod za dużym kątem
float d = distance(s.light.location, h.ip); // odległość ip od światła
ray shadowRay(h.ip, toLightDir); // promień cienia
hit obstacle = nearestHit(shadowRay, s); // testowanie zasłaniania światła
if (obstacle.t < d) // czy pewien obiekt zasłania światło?
return s.light.ambient; // tak, więc oświetlamy tylko światłem tła
else // nie, więc oświetlamy światłem tła + bezpośrednim
return s.light.ambient + s.light.intensity * cosNL;
} |
|
|








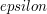 jest stałą dla błędów wynikających z zaokrągleń numerycznych.
Liczby zmiennoprzecinkowe mają niestety ograniczoną precyzję,
dlatego wyników działań na takich liczbach nie powinniśmy porównywać używając
bezpośredino operacji takich jak
jest stałą dla błędów wynikających z zaokrągleń numerycznych.
Liczby zmiennoprzecinkowe mają niestety ograniczoną precyzję,
dlatego wyników działań na takich liczbach nie powinniśmy porównywać używając
bezpośredino operacji takich jak 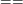 ,
, 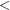 ,
, 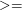 . Przykładowo, aby uniknąć
niepożądanych zjawisk, zwykle lepiej wykonać porównanie
. Przykładowo, aby uniknąć
niepożądanych zjawisk, zwykle lepiej wykonać porównanie 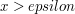 zamiast
zamiast 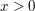 ,
bądź też uznać, że
,
bądź też uznać, że  jest równy zeru wtedy, gdy zachodzi
jest równy zeru wtedy, gdy zachodzi 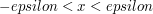 .
.
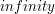 ,
i czasem będziemy sprawdzać czy pewna odległość jest mniejsza od nieskończoności.
Dodatkowo przyda się alias
,
i czasem będziemy sprawdzać czy pewna odległość jest mniejsza od nieskończoności.
Dodatkowo przyda się alias 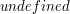 dla nieskończoności, którego będziemy używać do tego,
aby jawnie określać coś jako niezdefiniowane, co jednak może się zdefiniować w wyniku obliczeń,
które będą wykonywały zapytanie postaci
dla nieskończoności, którego będziemy używać do tego,
aby jawnie określać coś jako niezdefiniowane, co jednak może się zdefiniować w wyniku obliczeń,
które będą wykonywały zapytanie postaci 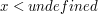 (jeśli
(jeśli 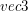 to element przestrzeni trójwymiarowej, czasami będzie symbolizował punkt, a czasami wektor,
stąd czwarty argument w jednym z konstruktorów tej struktury narzucający długość wektora.
to element przestrzeni trójwymiarowej, czasami będzie symbolizował punkt, a czasami wektor,
stąd czwarty argument w jednym z konstruktorów tej struktury narzucający długość wektora.
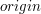 )
oraz z pary wektorów
)
oraz z pary wektorów 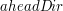 i
i 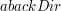 .
Oba wektory mają ten sam kierunek, ale przeciwne zwroty (tj.
.
Oba wektory mają ten sam kierunek, ale przeciwne zwroty (tj. 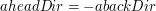 ).
).
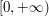 .
Dlaczego nie jest to trójka liczb z przedziału
.
Dlaczego nie jest to trójka liczb z przedziału ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) ?
Tutaj kolor jest synonimem energii, która jest nieujemna i może być dowolnie duża.
Dopiero chcąc przekształcić tą energię na kolor piksela będziemy musieli konwertować
nasz kolor do liczb z przedziału
?
Tutaj kolor jest synonimem energii, która jest nieujemna i może być dowolnie duża.
Dopiero chcąc przekształcić tą energię na kolor piksela będziemy musieli konwertować
nasz kolor do liczb z przedziału ![$ dr*cMap[i] $](/files/tex/4089c9a58322d2ac58e1f2f85eaf114a731d0cca.png) +
+ 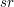 +
+ 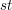
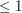 , gdzie
, gdzie  jest indeksem dowolnego teksela tekstury.
jest indeksem dowolnego teksela tekstury.  światłem punktowym. Zakładamy, że światło takie jest punktem
emitującym światło tak samo intensywne we wszystkich kierunkach. Natężenie światła reprezentujemy
jako kolor o składowych z przedziału
światłem punktowym. Zakładamy, że światło takie jest punktem
emitującym światło tak samo intensywne we wszystkich kierunkach. Natężenie światła reprezentujemy
jako kolor o składowych z przedziału 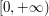 . Oprócz natężenia, które będzie odgrywało rolę
w bezpośrednim oświetleniu dajemy źródłu światła jeszcze jedną cechę - wkład w światło tła.
Jeżeli w pokoju jedynym źródłem światła jest lampa umieszczona przy suficie,
to światło z lampy nie dociera bezpośrednio np. pod stolik umieszczony w pokoju.
Wydawałoby się więc, że pod stolikiem powinna być całkowita ciemność,
a jednak tak nie jest. Dzieje się tak dlatego, że światło odbija się od innych obiektów
wpadając w przestrzeń pod stołem. Nie jest to łatwe do symulowania w sposób dokładny,
jednak można dokonać pewnego uproszczenia - założyć, że światło tła pochodzące ze
źródła światła jest stałe w całej scenie i doświetlić nim wszystkie obiekty sceny.
Dzięki temu w miejscach, gdzie światło nie dociera bezpośrednio,
nie będziemy mieli pełnych cieni w postaci czarnych plam.
. Oprócz natężenia, które będzie odgrywało rolę
w bezpośrednim oświetleniu dajemy źródłu światła jeszcze jedną cechę - wkład w światło tła.
Jeżeli w pokoju jedynym źródłem światła jest lampa umieszczona przy suficie,
to światło z lampy nie dociera bezpośrednio np. pod stolik umieszczony w pokoju.
Wydawałoby się więc, że pod stolikiem powinna być całkowita ciemność,
a jednak tak nie jest. Dzieje się tak dlatego, że światło odbija się od innych obiektów
wpadając w przestrzeń pod stołem. Nie jest to łatwe do symulowania w sposób dokładny,
jednak można dokonać pewnego uproszczenia - założyć, że światło tła pochodzące ze
źródła światła jest stałe w całej scenie i doświetlić nim wszystkie obiekty sceny.
Dzięki temu w miejscach, gdzie światło nie dociera bezpośrednio,
nie będziemy mieli pełnych cieni w postaci czarnych plam.
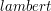 oblicza natężenie światła padające ze źródła światła na punkt
oblicza natężenie światła padające ze źródła światła na punkt 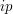 .
.  (z ilustracji) plus światło tła. Im wiekszy kąt padania światła, tym mniejsza jest intensywność światła padającego na punkt
(z ilustracji) plus światło tła. Im wiekszy kąt padania światła, tym mniejsza jest intensywność światła padającego na punkt 

