Podstawy algorytmów tekstowych
25.11.2009 - Damian Rusak
 AlfabetLimit czasowy : 1s; Limit pamięciowy : 16MB; Dla podanego alfabetu Wejście: Pierwsza linia wejścia zawiera dwie liczby naturalne Wyjście: Na wyjściu powinno znaleźć się Przykład: Wejście: 3 5 acb 4 abbc 6 adbdac 1 a 10 aaebbbaatb 3 abc Wyjście: TAK NIE TAK NIE TAK
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
PodsłowoLimit czasowy : 2s; Limit pamięciowy : 16MB; Dla podanych na wejściu dwóch słów, rozstrzygnij, czy pierwsze jest podsłowem drugiego, a jeśli tak, to na której pozycji rozpoczyna się wystąpienie tego słowa. Wejście: W pierwszej linii wejścia znajduje się liczba Wyjście: Dla każdego przypadku testowego należy wypisać na wyjście jedną linię - zawierającą wyraz "NIE", jeśli pierwsze słowo nie jest podsłowem drugiego, i "TAK", jeśli owym podsłowem jest. W przypadku wypisania "TAK", linia powinna zawierać także jedną liczbę naturalną - pozycję, na której zaczyna się podsłowo. Jeśli podsłowo występuje w kilku miejscach, wypisz najwcześniejszą pozycję. Kolejne symbole numerowane są od zera. Przykład: Wejście: 4 2 5 ab cabab 5 4 aaaaa aaaa 6 10 abcaaa abcabcaaar 4 4 dddd dddd Wyjście: TAK 1 NIE TAK 3 TAK 0
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Maksymalny prefikso - sufiksLimit czasowy : 1s; Limit pamięciowy : 16s; Dla danego słowa, oblicz długość jego maksymalnego prefikso-sufiksu - słowa, które jest zarazem jego prefiksem jak i sufiksem. Wejście: Pierwsza linia wejścia zawiera jedną liczbę naturalną Wyjście: W jedynej linii wyjścia powinna się znaleźć jedna liczba naturalna - długość maksymalnego właściwego (czyli nie równego całemu słowu) prefikso-sufiksu słowa z wejścia. Jeśli słowo nie posiada żadnego niepustego prefikso-sufiksu, należy wypisać 0. Przykład I : Wejście 6 aaaaaa Wyjście: 5 Maksymalny prefikso-sufiks - aaaaa Przykład II : Wejście: 12 aaabbaaabbaa Wyjście: 7 Maksymalny prefikso-sufiks - aaabbaa Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (10 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


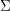 , rozstrzygnij, które słowa można utworzyć z symboli z
, rozstrzygnij, które słowa można utworzyć z symboli z  i
i  -
- 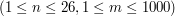 . W drugiej linii znajduje się w ciągu
. W drugiej linii znajduje się w ciągu 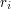 ,
, 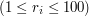 i słowie składającym się z małych liter alfabetu angielskiego, długości
i słowie składającym się z małych liter alfabetu angielskiego, długości  -ta linia powinna zawierać słowo "TAK" jeśli
-ta linia powinna zawierać słowo "TAK" jeśli 
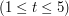 - ilość przypadków testowych. Kolejno następuje
- ilość przypadków testowych. Kolejno następuje 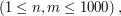 oznaczające długości kolejno pierwszego i drugiego słowa. W drugiej linii znajdują się dwa słowa oddzielone spacją. Słowa będą się składać jedynie z małych liter alfabetu angielskiego.
oznaczające długości kolejno pierwszego i drugiego słowa. W drugiej linii znajdują się dwa słowa oddzielone spacją. Słowa będą się składać jedynie z małych liter alfabetu angielskiego.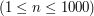 oznaczającą długość podanego słowa. W drugiej linii znajduje się słowo długości
oznaczającą długość podanego słowa. W drugiej linii znajduje się słowo długości 

