Podstawowe rozwiązanie
Zadanie polega na znalezieniu liczby różnych wspólnych niepustych podciągów trzech permutacji - kolejności slajdów wg Sławka, Hektora i Wiktora). Permutacja Sławka ma jednak postać 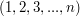 , co sprowadza powyższe do znalezienia liczby różnych wspólnych niepustych podciągów rosnących dwóch permutacji
, co sprowadza powyższe do znalezienia liczby różnych wspólnych niepustych podciągów rosnących dwóch permutacji 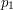 i
i 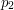 .
.
Dla każdego  niech
niech 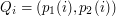 , czyli
, czyli 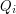 to para złożona z pozycji liczby
to para złożona z pozycji liczby  w obu permutacjach. Oznaczmy przez
w obu permutacjach. Oznaczmy przez 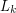 liczbę różnych wspólnych podciągów rosnących permutacji
liczbę różnych wspólnych podciągów rosnących permutacji 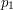 i
i 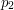 , których ostatnim wyrazem jest liczba
, których ostatnim wyrazem jest liczba  . Nietrudno zauważyć, że poszukiwana łączna liczba rosnących podciągów to
. Nietrudno zauważyć, że poszukiwana łączna liczba rosnących podciągów to 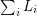 . Tak więc aby rozwiązać zadanie należy wyliczyć wartości
. Tak więc aby rozwiązać zadanie należy wyliczyć wartości 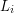 dla poszczególnych
dla poszczególnych  .
.
Zauważmy, że dla każdego  :
:
Powyższe zachodzi, gdyż każdy z ciągów kończących się na  jest albo ciągiem jednoelementowym (stąd jedynka przed sumą) albo przedłużeniem jakiegoś ciągu wyliczonego już wcześniej. Z tej równości otrzymujemy od razu algorytm działający w czasie
jest albo ciągiem jednoelementowym (stąd jedynka przed sumą) albo przedłużeniem jakiegoś ciągu wyliczonego już wcześniej. Z tej równości otrzymujemy od razu algorytm działający w czasie 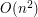 , który wystarczał do zdobycia większości punktów (7 lub 8 w zależności od implementacji). Bardziej zaawansowani zawodnicy mogli spróbować (i niektórym się udało) zaimplementować szybsze rozwiązanie.
, który wystarczał do zdobycia większości punktów (7 lub 8 w zależności od implementacji). Bardziej zaawansowani zawodnicy mogli spróbować (i niektórym się udało) zaimplementować szybsze rozwiązanie.
Szybsze rozwiązanie
Aby przyspieszyć powyższy algorytm skorzystamy z drzew przedziałowych. Właściwie same drzewa przedziałowe nie wystarczą, utworzymy drzewo przedziałowe drzew przedziałowych. W liściach drzewa nadrzędnego będziemy trzymać aktualne wartości 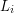 (na początku same zera) w kolejności posortowanej po pierwszej współrzędnej
(na początku same zera) w kolejności posortowanej po pierwszej współrzędnej 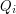 (czyli po
(czyli po 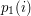 ). Każdy wewnętrzny węzeł drzewa nadrzędnego niech będzie drzewem przedziałowym złożonym z tych elementów, których odpowiadające liście są potomkami (być może dalekimi) danego węzła. Elementy wewnątrz każdego węzła są posortowane po drugiej współrzędnej
). Każdy wewnętrzny węzeł drzewa nadrzędnego niech będzie drzewem przedziałowym złożonym z tych elementów, których odpowiadające liście są potomkami (być może dalekimi) danego węzła. Elementy wewnątrz każdego węzła są posortowane po drugiej współrzędnej 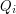 , czyli po
, czyli po 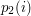 .
.
Wartości 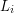 liczymy po kolei dla
liczymy po kolei dla 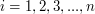 . Najpierw liczymy
. Najpierw liczymy 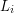 , a następnie obliczoną wartość
, a następnie obliczoną wartość 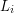 wstawiamy do drzewa nadrzędnego. Każda operacja wstawiania lub obliczania
wstawiamy do drzewa nadrzędnego. Każda operacja wstawiania lub obliczania 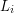 kosztuje
kosztuje 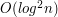 , gdyż odwołujemy się do
, gdyż odwołujemy się do 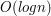 węzłów, a w każdym z węzłów wykonujemy
węzłów, a w każdym z węzłów wykonujemy 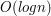 operacji. Złożoność całego algorytmu wynosi więc
operacji. Złożoność całego algorytmu wynosi więc 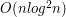 .
.


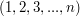 , co sprowadza powyższe do znalezienia liczby różnych wspólnych niepustych podciągów rosnących dwóch permutacji
, co sprowadza powyższe do znalezienia liczby różnych wspólnych niepustych podciągów rosnących dwóch permutacji 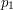 i
i 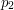 .
. niech
niech 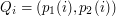 , czyli
, czyli 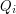 to para złożona z pozycji liczby
to para złożona z pozycji liczby 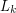 liczbę różnych wspólnych podciągów rosnących permutacji
liczbę różnych wspólnych podciągów rosnących permutacji  . Nietrudno zauważyć, że poszukiwana łączna liczba rosnących podciągów to
. Nietrudno zauważyć, że poszukiwana łączna liczba rosnących podciągów to 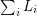 . Tak więc aby rozwiązać zadanie należy wyliczyć wartości
. Tak więc aby rozwiązać zadanie należy wyliczyć wartości 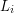 dla poszczególnych
dla poszczególnych 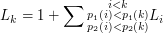
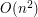 , który wystarczał do zdobycia większości punktów (7 lub 8 w zależności od implementacji). Bardziej zaawansowani zawodnicy mogli spróbować (i niektórym się udało) zaimplementować szybsze rozwiązanie.
, który wystarczał do zdobycia większości punktów (7 lub 8 w zależności od implementacji). Bardziej zaawansowani zawodnicy mogli spróbować (i niektórym się udało) zaimplementować szybsze rozwiązanie.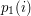 ). Każdy wewnętrzny węzeł drzewa nadrzędnego niech będzie drzewem przedziałowym złożonym z tych elementów, których odpowiadające liście są potomkami (być może dalekimi) danego węzła. Elementy wewnątrz każdego węzła są posortowane po drugiej współrzędnej
). Każdy wewnętrzny węzeł drzewa nadrzędnego niech będzie drzewem przedziałowym złożonym z tych elementów, których odpowiadające liście są potomkami (być może dalekimi) danego węzła. Elementy wewnątrz każdego węzła są posortowane po drugiej współrzędnej 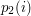 .
.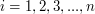 . Najpierw liczymy
. Najpierw liczymy 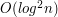 , gdyż odwołujemy się do
, gdyż odwołujemy się do 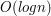 węzłów, a w każdym z węzłów wykonujemy
węzłów, a w każdym z węzłów wykonujemy 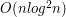 .
.









