Prestiż
05.06.2009
 Patrząc na przykład od razu widzimy, że wśród twierdzeń mogą być zarówno takie, które koniecznie trzeba udowodnić (oczywiście jeżeli zależy nam na rozwiązaniu całej teorii) jak i takie, które udowodnić co prawda można (i być może nawet prowadzi to do zwiększenia prestiżu), ale wcale nie trzeba. Na przykład jeżeli mamy twierdzenie B takie, że nie ma zależności typu "jeśli A to B", nikt go za nas nie udowodni, musimy więc zająć sie nim samemu (nawet jeżeli przez to już na każdej konferencji będą ścigały nas pogardliwe komentarze "patrzcie, to gość, który pokazał takie beznadziejne twierdzenie B!"). Z drugiej strony, jeżeli takie A istnieje, to równie dobrze możemy zająć sie nim zamiast B. Najłatwiej wyobrazić sobie całą sytuację tłumacząc oryginalny problem na język teorii grafów, na przykład w następujący sposób: mamy dany pewien graf skierowany, interesuje nas znalezienie takiego podzbioru jego wierzchołków X, że każdy inny wierzchołek jest z niego osiągalny. Tak naprawdę to interesuje nas znalezienie "najlepszego" takiego X, ale zastanówmy się najpierw jakie X są dobre (i miejmy nadzieje, że znalezienie najlepszego z nich okaże się już łatwe. No, a przynajmniej nie bardzo trudne). Jeżeli istnieje skierowana ścieżka z u do v, to oczywiście wystarczy, że w naszym zbiorze X będzie tylko u. Jeżeli istnieje też ścieżka w drugą stronę, z v do u, to obydwa te wierzchołki są tak samo "dobre", wystarczy wrzucić do X dowolny z nich. Ogólnie, jeżeli mamy zbiór wierzchołków o takiej własności, że między każdymi dwoma z nich da się przejść (w obydwie strony), to wystarczy nam wrzucenie do X tylko jednego z nich. Taki zbiór wierzchołków nazywa się zwykle silnie spójną składową (SSS). Skoro wiemy już, że z każdej SSS wystarczy nam wybranie tylko jednego wierzchołka, pozostaje już tylko zastanowić się, z których SSS rzeczywiście musimy wybrać przynajmniej jeden wierzchołek. Jeżeli w danej składowej S jest wierzchołek, do którego wchodzi krawędź mająca swój początek w innej składowej, to oczywiście nie musimy wybierać żadnego wierzchołka z S. Z drugiej strony, jeżeli takiej krawędzi nie ma, łatwo przekonać się o tym, że jakiś wierzchołek z S musimy wybrać (bo jest to jedyny możliwy sposób, w jaki możemy tam trafić). Takie SSS będziemy nazywali źródłami. W ten sposób otrzymaliśmy prostą charakteryzację "dobrych" zbiorów X: musimy wybrać przynajmniej jeden wierzchołek z każdego źródła. Tak naprawdę interesuje nas wybranie X o największym prestiżu (czyli średniej wadze), można więc od razu stwierdzić, że na pewno chcemy wybrać z każdego źródła wierzchołek o największej wadze. A co pozostałymi wierzchołkami? Tutaj mamy już pełną dowolność, każdy z nich możemy (niezależnie od innych) dodać do X lub też uznać, że nieszczególnie się to opłaca. Czyli tak naprawdę pokazaliśmy, że oryginalny problem można zredukować do następującego pytania: mamy dany dwie liczby p,q oraz zbiór A. Jak wybrać
Druga z nich nie wymaga głębszej refleksji: jedyny trudny kawałek to wyznaczenie silnie spójnych składowych. Możemy użyć albo opisanego w Cormenie algorytmu używającego dwóch przeszukiwań w głąb (jednego na pierwotnym grafie, drugiego na jego odwróconej kopii), lub (być może trochę sprytniejszej) wersji z tylko jednym przeszukiwaniem (tutaj). Co do pierwszej kwestii, zastanówmy się, czy byłoby łatwiej, gdyby ktoś podpowiedział nam, że najlepsze B ma k elementów. Pewnie byłoby: najlepiej wybrać największych elementów A. Niestety nie możemy liczyć na taką podpowiedź, musimy więc sprawdzać kolejno k=1,2,...,|A|. Jeżeli zamiast wybierać za każdym razem k największych elementów posortujemy A raz a dobrze, sprawdzenie każdej z możliwych wartości wykonamy w czasie stałym. Ostatecznie daje nam to złożoność Pozostaje jeszcze jedno pytanie: czy nie dałoby się lepiej? :) Wyznaczenie SSS wymaga tylko czasu Paweł Gawrychowski (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


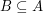 , które zmaksymalizuje
, które zmaksymalizuje 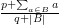 ? Pozostają więc tylko dwie kwestie:
? Pozostają więc tylko dwie kwestie: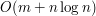 i 10 punktów.
i 10 punktów.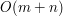 , jednak musieliśmy jeszcze posortować zbiór A, który mógł mieć aż
, jednak musieliśmy jeszcze posortować zbiór A, który mógł mieć aż  elementów. W ogólnym przypadku sortowanie takiego zbioru wymaga czasu
elementów. W ogólnym przypadku sortowanie takiego zbioru wymaga czasu 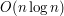 , jednak w tym konkretnym przypadku wszystkie jego elementu są liczbami całkowitymi z zakresu [-2000..2000]. Co oznacza, że tak naprawdę możemy zastąpić funkcję sort z biblioteki standardowej algorytmem liniowym (na przykład sortowaniem przez zliczanie). Nie jest to jednak zbyt ciekawa odpowiedź (z drugiej strony, może samo pytanie nie było zbyt ciekawe...). Załóżmy na chwilę, że prestiże poszczególnych twierdzeń mogą być dowolnie dużymi liczbami. Czy rzeczywiście potrzebne nam jest sortowanie? Okazuje się, że niekoniecznie, i że całą złożoność można zbić do
, jednak w tym konkretnym przypadku wszystkie jego elementu są liczbami całkowitymi z zakresu [-2000..2000]. Co oznacza, że tak naprawdę możemy zastąpić funkcję sort z biblioteki standardowej algorytmem liniowym (na przykład sortowaniem przez zliczanie). Nie jest to jednak zbyt ciekawa odpowiedź (z drugiej strony, może samo pytanie nie było zbyt ciekawe...). Załóżmy na chwilę, że prestiże poszczególnych twierdzeń mogą być dowolnie dużymi liczbami. Czy rzeczywiście potrzebne nam jest sortowanie? Okazuje się, że niekoniecznie, i że całą złożoność można zbić do 

