Zaginanie papieru (omówienie)
02.01.2012
Zadanie można było rozwiązać na wiele sposobów. W niniejszym omówieniu przedstawione będzie bardzo proste rozwiązanie osiągające złożoność czasową Zauważmy, że zagięcie papieru odpowiada "usunięciu" zaginanego fragmentu. Zauważmy też, że warunek o zaginaniu z lewej na prawą stronę jest bez znaczenia. Nasze rozwiązanie będzie bazowało na obserwacji (korzystającej z powyższych stwierdzeń), że najkrótszy końcowy fragment paska jaki można uzyskać przez zaginanie to pewne podsłowo wejściowego słowa zerojedynkowego. Zatem dla każdego podsłowa (przechodząc je od najkrótszych do najdłuższych) sprawdzamy, do jak małego podsłowa możemy je zagiąć. Rozwiązaniem będzie wynik dla całego paska. Niech słowo na wejściu to Zauważamy szybko, że 1. 2. 3. Aby przejrzeć możliwe wartości |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


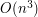 lub
lub 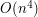 (w zależności od szczegółów implementacyjnych).
(w zależności od szczegółów implementacyjnych).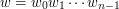 . Niech
. Niech 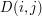 oznacza taką wartość dla
oznacza taką wartość dla 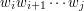 . Interesuje nas policzenie
. Interesuje nas policzenie 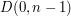 .
. 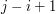
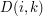 dla takich
dla takich 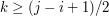 , że podsłowo
, że podsłowo 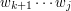 można nałożyć na słowo
można nałożyć na słowo 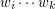 .
. 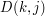 dla takich
dla takich 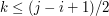 , że podsłowo
, że podsłowo 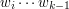 można nałożyć na słowo
można nałożyć na słowo  dla wszystkich podsłów potrzebujemy czasu rzędu
dla wszystkich podsłów potrzebujemy czasu rzędu 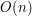 algorytmem Manachera albo w czasie
algorytmem Manachera albo w czasie 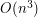 . Jeśli zdecydujemy się na brutalne porównania dla każdego podsłowa, okaże się, że złożoność osiągnie
. Jeśli zdecydujemy się na brutalne porównania dla każdego podsłowa, okaże się, że złożoność osiągnie 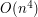 .
.









