Przewody (omówienie)
02.01.2012
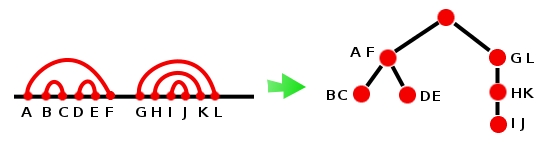
Zadanie można rozwiązać na wiele sposobów. W niniejszym omówieniu zostanie przedstawiona metoda, działająca w czasie Zauważmy, że przewody na górnej części płytki tworzą strukturę, którą można potraktować jak las (patrz ilustracja poniżej). Każdy kabel jest wierzchołkiem drzewa, połączonym z wierzchołkami, odpowiadającymi kablom, które są bezpośrednio "pod" nim (tj. gdyby narysować kable na kartce można by połączyć te dwa kable linią bez przecinania żadnych innych i jeden zamyka drugi poniżej). Taki las zamieniamy na drzewo dodając "super korzeń", który łączy wszystkie korzenie powstałych drzewek (jeśli jest ich więcej niż jedno).
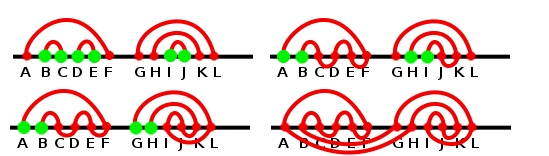
Utworzenie takiego drzewa wymaga jedynie czasu liniowego (łatwo jest za pomocą stosu zidentyfikować kable, które są bezpośrednio "obok" siebie). Wtedy łatwo już rozwiązać zadanie: przechodzimy drzewo w porządku post-order (czyli najpierw dzieci wierzchołka, potem sam wierzchołek, w razie nieznajomości tego pojęcia polecam sprawdzić w sieci). Dzięki temu będziemy łączyć części okablowania, idąc w górę drzewa. Zauważmy, że jeśli z każdego poddrzewa utworzymy kawałek, który jest krzywą z dwoma wolnymi końcami (tj. nie zablokowanymi przez kable, możliwymi do podłączenia do kabli spoza poddrzewa) to dla każdego wierzchołka drzewa wystarczy kolejno połączyć takie wolne końce od każdego z jego synów i zostawić dwa wolne końce dla swojego poddrzewa (patrz ilustracja poniżej). To wystarczy, aby doprowadzić do końca - dla "super korzenia" łączymy wreszcie dwa wolne końce ze sobą (na rysunku wolne końce są kolejno oznaczone na zielono).
Powyższe operacje wymagają też jedynie czasu liniowego. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


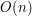 .
.