Schronisko - omówienie
14.12.2011
Zadanie było pomyślane jako najprostsze zadanie konkursowe i rzeczywiście prawie wszyscy zawodnicy rozwiązali je poprawnie. Na początek zauważmy, że jeśli co najmniej jeden bok prostokąta ma parzystą długość (mierzoną liczbą pól), to całą powierzchnię schroniska można pokryć śpiącymi turystami - wystarczy, że będziemy rozmieszczać turystów liniami równoległymy do boku parzystej długości. Każda linia będzie pokryta w całości i pokryjemy w ten sposób cały prostokąt. Przykładowo dla prostokąta o wymiarach 4x5 proces rozmieszczania turystów może wyglądać tak:
Pozostaje zastanowić się jak optymalnie zagospodarować prostokąt, którego oba boki mają długośc nieparzystą. Na pewno nie uda się go pokryć w całości, gdyż taki prostokąt zawiera nieparzystą liczbę pól, a każdy turysta potrzebuje dokładnie dwóch. Co najwyżej uda się więc pokryć wszystkie pola prostokąta poza jednym. I faktycznie takie rozmieszczenie jest zawsze możliwe. Wystarczy postępować analogicznie do metody dla prostokąta o parzystym boku, zostawiając jedną linię wolną. Na końcu uzupełniamy wolną linię turystami pozostawiając jedno puste pole. Przykładowo, dla prostokąta wymiarów 3x5:
W takim razie w pierwszym przypadku maksymalna liczba turystów, którzy mogą przenocować w schronisku wynosi |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


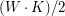 , a w drugim
, a w drugim