Kontynent (omówienie)
30.11.2011
W zadaniu podane są, w losowej kolejności, odcinki. Należy odtworzyć pola wielokątów przez nie tworzonych. Ograniczenia w zadaniu mówią, że każdy wielokąt jest prosty i bez dziur, podany zestaw odcinków może być więc interpretowany jako mapa państw bez enklaw. Podstawowym spostrzeżeniem pozwalającym na rozwiązanie tego zadania jest następujący fakt: odcinek S o jednym z końców w punkcie P oraz odcinek T o jednym z końców w punkcie P będący najbliżej na prawo odcinka S są kolejnymi bokami jednego z szukanych wielokątów. Ten fakt od razu nasuwa algorytm. W każdym z punktów sortujemy kątowo odcinki o jednym z końców w nim zawartych. Z każdego odcinka tworzymy dwa odcinki skierowane. Następnikiem odcinka skierowanego A -> B będzie taki odcinek B -> C, że BC jest pierwszym na prawo odcinkiem od odcinka BA (patrząc na odcinki zaczepione w punkcie B). Tak zdefiniowane następniki tworzą podział odcinków skierowanych na cykle, a każdy z takich cykli to jeden z szukanych wielokątów. Wystarczy teraz policzyć każdemu z wielokątów jego pole, na to jest już jednak gotowy wzór. Pole wielokąta o kolejnych wierzchołkach w punktach:
Wzór ten można uzasadnić faktem, że pole dowolnego wielokąta prostego bez dziur to suma pól (ze znakiem) trapezów o jednym z boków leżącym na osi X a drugim z boków będącym odcinkiem - bokiem wielokąta. Pole jednego takiego trapezu jest równe:
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


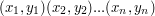 jest równe:
jest równe: 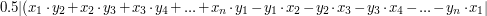
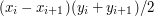 i jest ujemne, gdy wielokąt leży powyżej danego odcinka skierowanego (trzeba odjąć to, czego wcześniej dodaliśmy za dużo). Po zsumowaniu otrzymujemy podany wcześniej wzór na pole wielokąta.
i jest ujemne, gdy wielokąt leży powyżej danego odcinka skierowanego (trzeba odjąć to, czego wcześniej dodaliśmy za dużo). Po zsumowaniu otrzymujemy podany wcześniej wzór na pole wielokąta.









