Posłańcy
25.11.2011
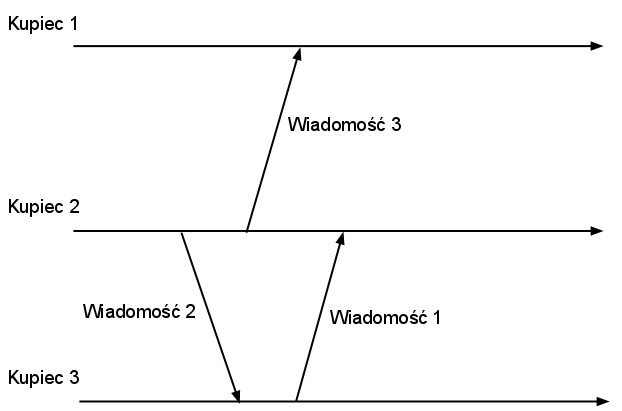
PosłańcyLimit czasowy: 5000 milisekund Dawno temu w pewnym królestwie żyło sobie N kupców. Kupcy zajmowali się w tym czasie tym samym, czym zajmują się dzisiaj - kupowaniem towarów jak najtaniej i sprzedawaniem ich jak najdrożej. Do robienia interesów służyły jednak inne narzędzia. Cała komunikacja pomiędzy kupcami odbywała się bowiem przy pomocy posłańców. Posłańcy przenoszą między kupcami wiadomości - każdą od dokładnie jednego kupca (nadawcy) do jednego innego (odbiorcy). W zależności od okoliczności, pogody, samopoczucia i kondycji posłańca, dostarczenie wiadomości może trwać chwilę, dłuższą chwilę, albo bardzo długo. Każdy z kupców dokumentuje swoją korespondencję odnotowując w dzienniku każdą wysłaną (natychmiast po wysłaniu) i każdą odebraną (natychmiast po odebraniu) wiadomość, zachowując kolejność chronologiczną. Tak więc każdy dziennik zawiera ciąg wydarzeń z których każde ma jedną z dwóch postaci:
Ze względu na brak precyzyjnych zegarów kupcy nie zapisują czasu w którym miały miejsce poszczególne wydarzenia.
Po kilku podejrzanych transakcjach (w szczególności po tym, jak kupiec Hektorino zainwestował duże środki w zakup winnic zaraz przed ogłoszeniem obniżki podatku na wino), królewscy kontrolerzy zaczęli podejrzewać niektórych kupców o nielegalne praktyki handlowe, szpiegostwo, oszustwo, spekulanctwo i chciwość. Król zarządził wielką kontrolę korespondencji kupców w celu ustalenia ciągu przyczynowo skutkowego pomiędzy wydarzeniami na rynku. Czy potrafisz napisać program, który znając zawartość dzienników korespondencji kupców będzie potrafił dla dowolnej pary wiadomości ustalić, która z nich była wysłana wcześniej? Uznajemy, że wiadomość a została wysłana przed wiadomością b, jeżeli istnieje ciąg wydarzeń (tj. wpisów w dziennikach kupców) x1, x2, ... , xk taki, że:
WejścieW pierwszej linii znajduje się liczba naturalna Z ( 1 <= Z <= 1 ) oznaczająca liczbę zestawów testowych. Następnie opisywane są kolejne zestawy. W pierwszej linii opisu pojedynczego zestawu testowego znajduje się para oddzielonych spacjami liczb naturalnych N i K ( 1 <= N <= 100; 1 <= K <= 100000) oznaczących - kolejno - liczbę kupców i liczbę zapytań. W kolejnych N liniach opisywane sa dzienniki poszczególnych kupców. Opis pojedynczego dziennika rozpoczyna się pojedynczą liczbą naturalną Si opisującą liczbę wydarzeń zapisanych w danym dzienniku. W dalszej kolejności wymieniane są poszczególne wydarzenia w danym dzienniku, jako ciąg Si oddzielonych spacjami liczb całkowitych w1, w2, ... , wk. Jeśli wi jest dodatnia, to oznacza wysłanie wiadomości o identyfikatorze wi. Jeśli wi jest ujemna, to oznacza odbiór wiadomości o identyfikatorze |wi|. Numer każdej wiadomości jest unikalny i należy zakresu od 1 do C, gdzie C oznacza liczbę wszystkich wiadomości wymienionych przez kupców. Numery wiadomości nie oznaczają kolejności ich wysyłania - służą wyłącznie jako identyfikatory. Liczba C nie jest wprost podana na wejściu, ale gwarantujemy, że będzie należeć do zakresu od 1 do 100000. W kolejnych K liniach opisywane są zapytania. Każde zapytanie ma postać pary identyfikatorów dwóch różnych wydarzeń oddzielonych pojedynczą spacją. Gwarantujemy, że dane wejściowe nie będą prowadzić do sprzeczności, czyli do wywnioskowania dla jakiejkolwiek pary wiadomości a, b, że a została wysłana przed b oraz b została wysłana przed a. WyjścieDla każdego zestawu testowego należy w K liniach wypisać odpowiedzi na poszczególne zapytania. Dla każdego zapytania należy wypisać identyfikator wiadomości, która została wysłana jako pierwsza, lub znak zapytania, jeśli na podstawie wpisów w dziennikach kupców nie da się ustalić kolejności. Przykład
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com