Rendering wolumetryczny
20.12.2010 - Adam Błaszkiewicz
   Krok 1 - Generowanie promieni głównych
Przez promienie główne rozumiemy promienie wystrzelone z kamery w stronę każdego piksela. Kamera zdefiniowana jest jako macierz transformująca widok z punktu
Natomiast jeśli przemnożymy wektor Na początku wygenerujemy promienie główne dla wspomnianego wcześniej widoku ze środka układu współrzędnych, a następnie przemnożymy je przez macierz kamery, aby otrzymać właściwy już widok. Obszar widziany przez kamerę ma kształt ostrosłupa o prostokątnej podstawie - kamera jest jego czubkiem. Właściwie, jego wysokość powinna być nieskończona, w ten sposób, że nigdy nie dotrzemy do podstawy. Wyobraźmy sobie, że w którymś miejscu przetniemy nasz ostrosłup płaszczyzną - możemy sobie wyobrazić, że to będzie ekran, na który powinien być rzutowany każdy punkt przestrzeni znajdujący się w ostrosłupie, wzdłuż prostej przechodzącej przez ten punkt i przez kamerę (wierzchołek ostrosłupa). Dla ułatwienia, przetniemy ostrosłup w odległości 1 od kamery.
Sam kształt ostrosłupa determinowany jest kątem widzenia kamery w pionie (ang. FOV - Field of view) oraz stosunkiem szerokości do wysokości ekranu (ang. Aspect ratio). Kąt widzenia w pionie jest oznaczony na rysunku jako
Aby wygenerować promień, należy dodać do siebie
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


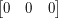 w stronę dodatniej osi Z. Tak więc po pomnożeniu wektora
w stronę dodatniej osi Z. Tak więc po pomnożeniu wektora 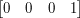 przez taką macierz, otrzymamy pozycję kamery.
przez taką macierz, otrzymamy pozycję kamery.
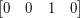 przez tę samą macierz, dostaniemy kierunek, w którym kamera jest skierowana.
przez tę samą macierz, dostaniemy kierunek, w którym kamera jest skierowana.
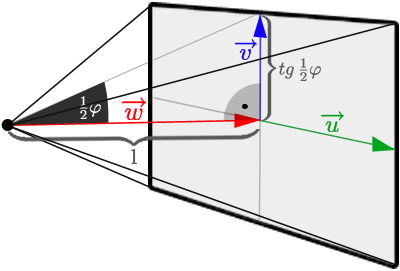
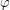 . Widać, że długość wektora
. Widać, że długość wektora  wynosi
wynosi 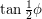 . Długość wektora
. Długość wektora  można obliczyć, mnożąc długość
można obliczyć, mnożąc długość 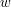 oraz przemnożone przez skalary z zakresu
oraz przemnożone przez skalary z zakresu ![$ [-1,1] $](/files/tex/597c956c92d65b2835e8fcfb93ac089f06479db4.png)
 ).
).


