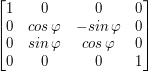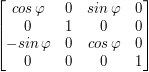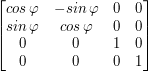Krok 0 - Wektory i macierze
Do transformacji punktów w przestrzeni trójwymiarowej normalnie należałoby użyć wektorów trójwymiarowych i macierzy 3x3, jednak nie mielibyśmy wtedy możliwości translacji (przesuwania) punktów. Dlatego powszechnie używa się w tym celu wektorów czterowymiarowych i macierzy 4x3. Wektory trójwymiarowe 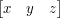 reprezentujemy w takim wypadku jako
reprezentujemy w takim wypadku jako 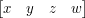 , dla pewnego
, dla pewnego 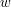 , np.
, np. 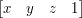 . Ta ostatnia jedynka pozwala nam na utworzenie macierzy, która dodaje do danego wektora pewien stały wektor (przemnożony przez tę jedynkę) - a więc macierz translacji.
. Ta ostatnia jedynka pozwala nam na utworzenie macierzy, która dodaje do danego wektora pewien stały wektor (przemnożony przez tę jedynkę) - a więc macierz translacji.
Mnożąc wektor 4-wymiarowy przez macierz 4x3 otrzymalibyśmy wektor 3-wymiarowy:
Wektor wynikowy ma tylko 3 wymiary, ale będziemy go konwertować z powrotem do postaci 4-wymiarowej, przepisując 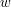 bez zmian. Taki sam efekt osiągnęlibyśmy rozszerzając macierz do wymiarów 4x4 trzema zerami i jedynką, jak w macierzy identycznościowej:
bez zmian. Taki sam efekt osiągnęlibyśmy rozszerzając macierz do wymiarów 4x4 trzema zerami i jedynką, jak w macierzy identycznościowej:
Dlatego, z matematycznego punktu widzenia, będziemy operować na macierzach 4x4, chociaż w implementacji będą to tylko macierze 4x3:
1
2
3
4
5
6
7
8
9
10
11
| class Matrix
{
public Matrix()
{
vals = new double[4,3];
}
// (...)
protected double[,] vals;
} |
Mnożenie macierzy również tak naprawdę mnoży dwie macierze 4x4, jednak w implementacji lepiej mnożyć macierz 4x3 przez macierz 3x3 i ręcznie dodać czwarty wiersz drugiej macierzy (przed przycięciem) do wyniku - można sprawdzić, że jest to równoważne:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Matrix
{
// (...)
public static Matrix operator *(Matrix a, Matrix b)
{
Matrix r = new Matrix();
for (int i = 0; i < 4; ++i)
{
for (int k = 0; k < 3; ++k)
{
for (int j = 0; j < 3; ++j)
{
r.vals[i, j] += a.vals[i, k] * b.vals[k, j];
}
}
}
r.vals[3, 0] += b.vals[3, 0];
r.vals[3, 1] += b.vals[3, 1];
r.vals[3, 2] += b.vals[3, 2];
return r;
}
// (...)
} |
Będziemy korzystać z dwóch typów wektorów - wektory kierunku i wektory pozycji. Wektor kierunku jest postaci 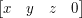 , a wektor pozycji
, a wektor pozycji 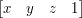 . W ten sposób wektory kierunku będą ignorowały ostatni wiersz macierzy, czyli translację.
. W ten sposób wektory kierunku będą ignorowały ostatni wiersz macierzy, czyli translację.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Vector
{
// (...)
public static Vector operator *(Vector v, Matrix m)
{
Vector r = new Vector();
r.x = v.x * m[0, 0] + v.y * m[1, 0] + v.z * m[2, 0] + m[3, 0];
r.y = v.x * m[0, 1] + v.y * m[1, 1] + v.z * m[2, 1] + m[3, 1];
r.z = v.x * m[0, 2] + v.y * m[1, 2] + v.z * m[2, 2] + m[3, 2];
return r;
}
// (...)
}
// (...)
class DirectionVector : Vector
{
public static DirectionVector operator *(DirectionVector v, Matrix m)
{
DirectionVector r = new DirectionVector();
r.x = v.x * m[0, 0] + v.y * m[1, 0] + v.z * m[2, 0];
r.y = v.x * m[0, 1] + v.y * m[1, 1] + v.z * m[2, 1];
r.z = v.x * m[0, 2] + v.y * m[1, 2] + v.z * m[2, 2];
return r;
}
} |
Macierze, których będziemy używać
- Oczywiście macierz identycznościowa
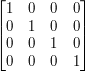
1
2
3
4
5
6
7
8
9
10
11
| class IdentityMatrix : Matrix
{
public IdentityMatrix()
: base()
{
vals[0, 0] = 1.0;
vals[1, 1] = 1.0;
vals[2, 2] = 1.0;
// Pamiętamy, że przechowujemy tylko 3 pierwsze kolumny macierzy
}
} |
- Wspomniana wcześniej macierz translacji
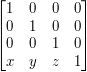 - przesuwa punkt o wektor
- przesuwa punkt o wektor 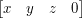 .
.
1
2
3
4
5
6
7
8
9
10
| class TranslationMatrix : IdentityMatrix
{
public TranslationMatrix(double x, double y, double z)
: base()
{
vals[3, 0] = x;
vals[3, 1] = y;
vals[3, 2] = z;
}
} |
- Macierze obrotów - obracają punkt wokół odpowiedniej osi o kąt 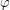 .
.
- Wokół osi X -
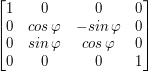
- Wokół osi Y -
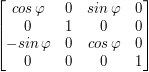
- Wokół osi Z -
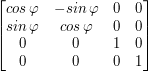
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class XRotationMatrix : IdentityMatrix
{
public XRotationMatrix(double angle)
: base()
{
vals[1, 1] = vals[2, 2] = Math.Cos(angle);
vals[2, 1] = Math.Sin(angle);
vals[1, 2] = -vals[2, 1];
}
}
class YRotationMatrix : IdentityMatrix
{
public YRotationMatrix(double angle)
: base()
{
vals[0, 0] = vals[2, 2] = Math.Cos(angle);
vals[0, 2] = Math.Sin(angle);
vals[2, 0] = -vals[0, 2];
}
}
class ZRotationMatrix : IdentityMatrix
{
public ZRotationMatrix(double angle)
: base()
{
vals[0, 0] = vals[1, 1] = Math.Cos(angle);
vals[1, 0] = Math.Sin(angle);
vals[0, 1] = -vals[1, 0];
}
} |
Dodatkowo wprowadzamy dla ułatwienia macierz obracającą punkt wokół wszystkich trzech osi po kolei - yaw (Y), pitch (X), roll (Z). Implementujemy taki obrót najprościej, jak tylko się da - przez wymnożenie trzech macierzy obrotów, odpowiednio wokół osi X, Y, Z.
1
2
3
4
5
6
7
8
9
10
| class ZXYRotationMatrix
{
static public Matrix New(double z, double x, double y)
{
Matrix zm = new ZRotationMatrix(z);
Matrix xm = new XRotationMatrix(x);
Matrix ym = new YRotationMatrix(y);
return zm * xm * ym;
}
} |





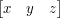 reprezentujemy w takim wypadku jako
reprezentujemy w takim wypadku jako 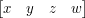 , dla pewnego
, dla pewnego 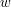 , np.
, np. 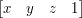 . Ta ostatnia jedynka pozwala nam na utworzenie macierzy, która dodaje do danego wektora pewien stały wektor (przemnożony przez tę jedynkę) - a więc macierz translacji.
. Ta ostatnia jedynka pozwala nam na utworzenie macierzy, która dodaje do danego wektora pewien stały wektor (przemnożony przez tę jedynkę) - a więc macierz translacji.


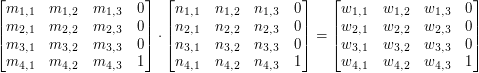
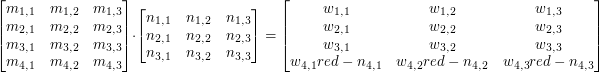
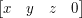 , a wektor pozycji
, a wektor pozycji 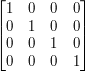
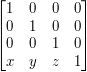 - przesuwa punkt o wektor
- przesuwa punkt o wektor 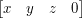 .
.
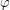 .
.