Bezstratna kompresja dźwięku
28.07.2010 - Krzysztof Templin
  Kodowanie predykcyjneSpróbujemy nieco poprawić osiągi naszego kodeka. Obserwując z bliska cyfrowy zapis fali dźwiękowej, można zauważyć, że często na podstawie kilku kolejnych próbek można wyciągnąć pewne wnioski na temat następnej próbki. Przykładowo, bardzo często wartość próbki jest nieodległa od wartości próbki poprzedzającej. Ciąg W możemy przekształcić w ciąg różnic D zdefiniowany następująco: D[0] = W[0], Zauważmy, że ciąg W łatwo jest odtworzyć na podstawie ciągu D. Jeśli porównamy teraz rozkłady wartości ciągów W i D (rys. 4 i rys.5), zauważymy, że wartości po przekształceniu „przesunęły się” w kierunku zera. Przedstawione wyżej kodowanie różnicowe jest szczególnym przypadkiem ogólniejszej metody, zwanej kodowaniem predykcyjnym. W metodzie tej wybieramy pewną funkcję (predyktor), której zadaniem jest „przewidywanie” wartości i-tej próbki na podstawie próbek o numerach mniejszych niż i. Następnie zamiast właściwego ciągu próbek, zapamiętujemy ciąg błędów szacowania przy pomocy obranego predyktora. Formalnie, kodowaniem predykcyjnym sygnalu W przy użyciu predyktora p, nazywamy ciąg E, zdefiniowany następująco: E[i] = W[i] − p(i). Oczywiście kodowanie to jest odwracalne: wystarczy przetwarzać wartości zakodowanego ciągu w kolejności rosnących indeksów dodając odpowiednią wartość p. PRZYKŁAD. Niech p(i) = 0 dla dowolnego i. Wtedy oczywiście sygnał jest swoim własnym kodowaniem, tj. E = W. PRZYKŁAD. Niech p(0) = 0, p(i) = W[i−1] (i > 0). W tym przypadku mamy do czynienia z kodowaniem różnicowym, czyli E = D. PRZYKŁAD. Niech p(0) = p(1) = 0, p(i) = 2W[i−1] − W[i−2] (i > 1). Szacujemy, że każda z próbek leży na przedłużeniu prostej przechodzącej przez dwie poprzednie próbki.
Intuicja, która stoi u podstaw stosowania kodowania predykcyjnego jest następująca: wartości sąsiednich próbek są między sobą skorelowane; w zapisie muzyki pewne następstwa próbek są mniej prawdopodobne niż inne. Zatem opis, w którym każda próbka jest zapisywana niezależnie powoduje zduplikowanie części informacji zawartej w sygnale. Staramy się więc pozbyć nadmiarowej informacji, licząc na to, że później uda nam się zapisać sygnał używając mniejszej liczby bitów.
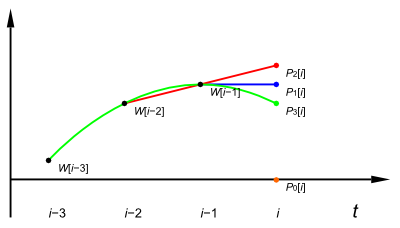
Rysunek 6. Działanie predyktorów z rodziny P. Celem, do którego zmierzamy jest zastosowanie możliwie dobrego kodowania predykcyjnego przed kodowaniem prefiksowym, dzięki czemu średnia długość kodu ulegnie skróceniu. W naszym przypadku najlepsze kodowanie predykcyjne to takie, które skraca długość nastepującego po nim kodowania Rice'a, ale my trochę uprościmy sobie zadanie i przyjmiemy następującą heurystykę: najlepsze kodowanie predykcyjne to takie, dla którego średni błąd (co do wartości bezwzględniej) jest najmniejszy. A zatem chcemy zminimalizować wyrażenie: |E[0]| + |E[1]| + |E[2]| + … Wspomniane wcześniej przykłady predyktorów, to trzy pierwsze funkcje z rodziny predyktorów wielomianowych P. W rodzinie tej predyktor Pi (i > 0) jest wielomianem stopnia i-1 przechodzącym przez i ostatnich punktów. P0 to wielomian zerowy. W naszym kodeku będziemy wybierać spośród predyktorów P0, P1, P2 oraz P3 zilustrowanych na rysunku 6. ImplementacjaW ogólnym zarysie, algorytm kompresji polega na wykonaniu następujących kroków:
Oczywiście, dekompresja polega na odwróceniu całego procesu. Więcej wynikówW tabeli 2 przedstawiono wyniki kodeka po dodaniu kodowania predykcyjnego. Przykłady muzyczne jak poprzednio. Dla porównania zamieszczono również wyniki działania kodeka FLAC.
Tabela 2. Ostateczne wyniki działania kodeka i porównanie z FLAC. Trzeba przyznać, że stopień kompresji nie jest imponujący, zwłaszcza gdy weźmie się pod uwagę wyniki osiągane przez kodeki stratne, takie jak MP3. Zauważmy jednak, że dość prostymi środkami osiągnęliśmy wyniki niewiele gorsze od kodeka FLAC. W istocie, to co zaimplementowaliśmy, to zasadnicza część metod stosowanych przez FLAC. Porównanie wyników popularnych bezstratnych kodeków [4] pokazuje, że zejście poniżej 50-procentowej kompresji przeważnie pozostaje poza naszym zasięgiem. Możliwości dalszego rozwojuObsługa szczególnych wypadków: 1. Wykrywać obszary, gdzie wartość próbek jest stała (cisza) i kodować je w stałej pamięci. Poprawa efektywności i nowe funkcje: 3. Przyspieszyć działanie kodeka (być może poprzez przepisanie go z Pythona do C).  Kod źródłowy kodeka w PythonieBibliografia[1] Tony Robinson. SHORTEN: Simple lossless and near-lossless waveform compression. [2] Mat Hans, Ronald W. Schafer. Lossless Compression of Digital Audio. [3] FLAC Format Specification. http://flac.sourceforge.net/format.html [4] http://flac.sourceforge.net/comparison_all_ratio.html [5] Wikipedia http://en.wikipedia.org/wiki/Quantization_(signal_processing)
(3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


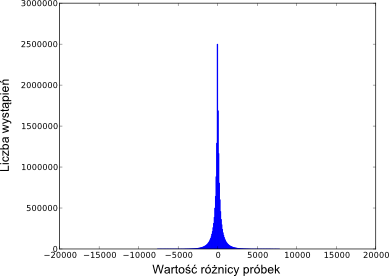 Rysunek 5. Rozkład wartości ciągu D dla przykładowego pliku muzycznego.
Rysunek 5. Rozkład wartości ciągu D dla przykładowego pliku muzycznego.