Bezstratna kompresja dźwięku
28.07.2010 - Krzysztof Templin
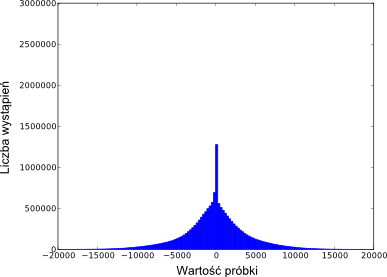
  Kodowanie prefiksoweW zapisie stosowanym na płycie CD-Audio, zapamiętanie każdej z 216 możliwych wartości pojedynczej próbki wymaga dokładnie 16 bitów. Możemy jednak zastosować kodowanie, w którym długość kodu jest zmienna. Oznacza to, że niektóre liczby będą zapisywane przy pomocy mniejszej niż 16 liczby bitów, a inne większej. Jeśli w ciągu wejściowym wartości o krótszych kodach występują odpowiednio często, średnia długość kodu będzie mniejsza niż 16 i otrzymamy w wyniku ciąg o krótszej długości. Należy przy tym jednak zwrócić uwagę na istotny aspekt takiego podejścia: jeśli wypiszemy ciąg bitów powstały poprzez sklejenie kolejnych kodów, to skąd będziemy wiedzieć, gdzie leżą granice między kodami? Do tej pory sprawa była prosta: granice były rozłożone równomiernie co 16 bitów. Teraz sprawy się komplikują. Aby zaradzić temu problemowi, narzucimy pewne ograniczenie na kody. Otóż żaden kod nie może być prefiksem innego kodu. Dzięki temu, jeśli na początku ciągu bitów rozpoznamy jakiś kod, możemy być pewni, że koduje on pierwszą próbkę, gdyż wszystkie dłuższe kody zaczynają się w inny sposób. Czytając zatem ciąg od lewej do prawej możemy bez problemu odkodować cały blok. Kodowanie z powyższym ograniczeniem nosi miano prefiksowego. Kody Rice'aNa rysunku 4 widzimy przykładowy rozkład wartości próbek w pliku dźwiękowym. Widać wyraźnie, że wartości o większej wartości bezwzględnej występują (z grubsza) rzadziej. W naszym kodeku posłużymy się takim kodowaniem prefiksowym, które wykorzystuje tę obserwację. Co prawda nie osiąga ono największej możliwej kompresji, jednakże jest bardzo proste w implementacji.
Rysunek 4. Rozkład wartości próbek w przykładowym pliku muzycznym. Zapis, którego użyjemy, nosi nazwę kodów Rice'a. Niech d będzie pewną ustaloną liczbą naturalną i przypuśćmy, że chcemy zakodować liczbę naturalną n. Możemy jednoznacznie wskazać liczby naturalne q oraz r (r < 2d) takie, że n = q2d + r. (Są to odpowiednio iloraz i reszta z dzielenia całkowitego n przez 2d.) Kod Rice'a liczby n konstruujemy następująco: wypisujemy q zer, potem jedynkę, a na końcu zwyczajny zapis binarny liczby r, na który potrzebujemy d bitów. PRZYKŁAD. Niech d = 3 i n = 14. Wtedy n = 1 × 23 + 6, zatem kod to 01110. PRZYKŁAD. Niech d = 2 i n = 40. Wtedy n = 10 × 22 + 0, zatem kod to 0000000000100. PRZYKŁAD. Niech d = 10 i n = 1. Wtedy n = 0 × 210 + 1, zatem kod to 10000000001. Zauważmy, że przy ustalonym parametrze d długości kodów rosną wraz z wartością liczby n. Kodowanie to pozwala zapisywać jedynie liczby naturalne, więc wcześniej do ciągu wejściowego zaaplikujemy wzajemnie jednoznaczne przekształcenie f: Z → N: f(n) = 2n, dla n nieujemnych, W ten sposób liczbom o mniejszym module przypiszemy krótsze kody. W istocie należałoby przeprowadzić głębszą analizę, dlaczego akurat kodowanie Rice'a jest korzystne w naszym przypadku, jednak zadanie to wykracza poza ramy niniejszego artykułu. Zainteresowanym czytelnikom polecam zapoznanie się z bibliografią. Do ustalenia pozostała jeszcze jedna kwestia: wybór parametru d. Na pewno nie ma sensu stosować d większego niż 15. Ograniczenie to jest na tyle niewielkie, że nasz kodek może po prostu sprawdzić każdą możliwość i wybrać najlepszą z nich. Pierwsze wynikiW tabeli 1 przedstawiono wyniki działania kodeka stosującego podział na bloki długości 1000 i kodowanie Rice'a na 3 przykładach:
Tabela 1. Pierwsze wyniki działania kodeka. (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com