Wielki przełom
Czy już widzicie, że jesteśmy gotowi do napisania naszego algorytmu? Umiemy już szybko liczyć ![$ Q[j][n+1] $](/files/tex/9beded3ddb0e3d5687f2f9a67eea346c452c9136.png) , mając wcześniej policzone
, mając wcześniej policzone ![$ Q[i][n] $](/files/tex/9233f981a245075c883862adef84c198857c757b.png) dla wszystkich monet
dla wszystkich monet  . To pozwoli nam zapisać następujący algorytm:
. To pozwoli nam zapisać następujący algorytm:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| Argumenty:
x[1...T] = wyrzucone monety
n = liczba wszystkich monet
p[1...n][1...n] = prawdopodobieństwo przejścia z monety i do j
w[orzeł, reszka][1...n] = prawdopodobieństwo wyrzucenia x za pomocą monety i
Inicjalizacja:
Dla wszystkich monet m:
Q[m][1] = prawdopodobieństwo zaczęcia monetą m
T[m][1] = Lista składająca sie tylko z monety m
Dla k = 2...T
Dla m = 1...n
Policz Q[m][k]:
Policz Q[j][k-1] * p[j][m] * w[m][ x[k] ] dla wszystkich monet j
i = moneta dla której Q[j][k-1] * p[j][m] * w[m][ x[k] ] jest największe
Q[m][k] = Q[i][k-1] * p[i][m] * w[m][ x[k] ]
T[m][k] = lista T[i][k-1] z dołączoną monetą m na przedzie |
Dla każdego k i dla każdej monety m
wyznacza on ciąg monet , które najlepiej tłumaczy wyniki rzutów 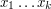 przy założeniu, że ostatnim rzucie skorzystano z monety
przy założeniu, że ostatnim rzucie skorzystano z monety  . W ten sposób
udało się nam znaleźć ciąg monet, który najlepiej tłumaczy wyniki wszystkich rzutów
. W ten sposób
udało się nam znaleźć ciąg monet, który najlepiej tłumaczy wyniki wszystkich rzutów
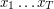 .
.
Jak szybki jest ten algorytm? Żeby odpowiedzieć na to pytanie wystarczy
przeanalizować jego główną pętlę. Żeby policzyć Q[m][k] dla konkretnego  potrzeba
potrzeba 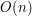 operacji (n to liczba monet), bo musimy policzyć
operacji (n to liczba monet), bo musimy policzyć
![$ Q[j][k-1] \cdot p[j][m] \cdot w[m][ x[k] ] $](/files/tex/9225e79c06bc8e30febe1d03ff83b4e1a224a757.png) dla wszystkich monet
dla wszystkich monet  .
.
Jeżeli weźmiemy pod uwagę pętle wewnątrz których jest operacja liczenia Q[m][k],
okaże się, że łączna złożoność algorytmu to 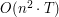 . Oznacza to, że
jest liniowy względem liczby wyników rzutów monetą, a kwadratowy względem
liczby monet.
. Oznacza to, że
jest liniowy względem liczby wyników rzutów monetą, a kwadratowy względem
liczby monet.





![$ Q[j][n+1] $](/files/tex/9beded3ddb0e3d5687f2f9a67eea346c452c9136.png) , mając wcześniej policzone
, mając wcześniej policzone ![$ Q[i][n] $](/files/tex/9233f981a245075c883862adef84c198857c757b.png) dla wszystkich monet
dla wszystkich monet  . To pozwoli nam zapisać następujący algorytm:
. To pozwoli nam zapisać następujący algorytm:
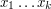 przy założeniu, że ostatnim rzucie skorzystano z monety
przy założeniu, że ostatnim rzucie skorzystano z monety  . W ten sposób
udało się nam znaleźć ciąg monet, który najlepiej tłumaczy wyniki wszystkich rzutów
. W ten sposób
udało się nam znaleźć ciąg monet, który najlepiej tłumaczy wyniki wszystkich rzutów
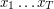 .
.
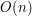 operacji (n to liczba monet), bo musimy policzyć
operacji (n to liczba monet), bo musimy policzyć
![$ Q[j][k-1] \cdot p[j][m] \cdot w[m][ x[k] ] $](/files/tex/9225e79c06bc8e30febe1d03ff83b4e1a224a757.png) dla wszystkich monet
dla wszystkich monet  .
.
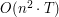 . Oznacza to, że
jest liniowy względem liczby wyników rzutów monetą, a kwadratowy względem
liczby monet.
. Oznacza to, że
jest liniowy względem liczby wyników rzutów monetą, a kwadratowy względem
liczby monet.


