Zabawa wzorami dla ekspertów
Teraz zabierzemy się za drugą część. Na początek utrudnijmy sobie zadanie. Załóżmy, że Jaś rzucał monetą  razy i uzyskał wyniki
razy i uzyskał wyniki 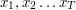 .
Jaki jest najbardziej prawdopodobny ciąg monet? Najprostszym sposobem, żeby go wyznaczyć jest następujący algorytm:
.
Jaki jest najbardziej prawdopodobny ciąg monet? Najprostszym sposobem, żeby go wyznaczyć jest następujący algorytm:
1
2
3
| Dla każdego ciągu ciągu monet o długości T:
Wyznacz prawdopodobieństwo tego ciągu
Zwróć najbardziej prawdopodobny ciąg |
Domyślamy się, że policzyć prawdopodobieństwo tego, że rzucano konkretnym ciągiem monet.
Niestety, wszystkich możliwych ciągów jest 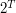 (mamy
(mamy  miejsc, na każde wstawiamy jedną z dwóch monet).
I wszystkie musimy sprawdzić. To zdecydowanie za dużo. Dlatego, zaraz zobaczymy dużo szybszy algorytm.
miejsc, na każde wstawiamy jedną z dwóch monet).
I wszystkie musimy sprawdzić. To zdecydowanie za dużo. Dlatego, zaraz zobaczymy dużo szybszy algorytm.
Nasz algorytm będzie tak dobry, że poradzi sobie nawet z trudniejszym zadaniem. Mianowicie takim, w którym Jaś ma do dyspozycji  monet zamiast dwóch. Dane wejściowe tego algorytmu to:
monet zamiast dwóch. Dane wejściowe tego algorytmu to:
- Tablica w[i][k], mówiąca, jakie jest prawdopodobieństwo wrzucenia
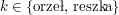 monetą
monetą  :
:
![$ w[i][k] = P( \mbox{ Jaś wyrzuci k} | \mbox{ Jaś rzuca monetą i} ) $](/files/tex/b9624b2a8e5113f2197905958fece6d0dab27205.png) ,
,
- Tablica p[i][j], mówiąca, jakie jest prawdopodobieństwo tego, że Jaś w następnej turze będzie rzucał monetą
 , jeżeli w tej turze rzuca monetą
, jeżeli w tej turze rzuca monetą  .
.
Nasz algorytm będzie tworzył dwie tablice. Pierwsza z nich, ![$ L[i][n] $](/files/tex/249450c06a1e1d1e6fd851d25fcef72a2c7186bc.png) będzie przechowywała najbardziej prawdopodobny ciąg monet
będzie przechowywała najbardziej prawdopodobny ciąg monet 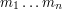 kończący się monetą
kończący się monetą  (to znaczy
(to znaczy 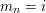 ).
Innymi słowy, chodzi o ciąg, który maksymalizuje prawdopodobieństwo
).
Innymi słowy, chodzi o ciąg, który maksymalizuje prawdopodobieństwo 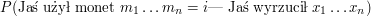 .
.
Teraz zobaczymy coś ciekawego. Z właściwości prawdopodobieństwa warunkowego wiemy, że:
jest równe:
Zauważmy, że mianownik
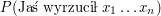
jest niezależny od ciągu monet. To oznacza, że ciąg monet, który maksymalizuje
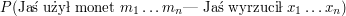
, maksymalizuje również
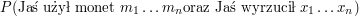
.
To drugie wyrażenie okaże się łatwiejsze do wyliczenie i dlatego w tablicy ![$ Q[j][n] $](/files/tex/9d680455008a934b82638b64eec164bd1a7a6d73.png) będziemy przechowywali właśnie
będziemy przechowywali właśnie 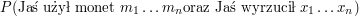 ,
gdzie
,
gdzie 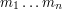 jest ciągiem monet, który trzymamy w tablicy
jest ciągiem monet, który trzymamy w tablicy ![$ W[j][n] $](/files/tex/0a89f857bb812b242674267218a518369f434964.png) . Czyli maksymalizującym zarówno
. Czyli maksymalizującym zarówno
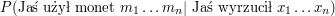 jak i
jak i 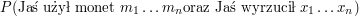 .
.
Jeżeli uda nam się wyznaczyć wartości w tablicach ![$ Q[j][n] $](/files/tex/9d680455008a934b82638b64eec164bd1a7a6d73.png) i
i ![$ W[j][n] $](/files/tex/0a89f857bb812b242674267218a518369f434964.png) dla wszystkich wszystkich monet (a więc dla każdego
dla wszystkich wszystkich monet (a więc dla każdego  ) oraz dla
) oraz dla
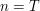 (liczba wszystkich rzutów monetą), to nasze zadanie będzie skończone.
Wystarczy wybrać to
(liczba wszystkich rzutów monetą), to nasze zadanie będzie skończone.
Wystarczy wybrać to  dla którego
dla którego ![$ Q[j][T] $](/files/tex/c5f2f4c4b2089b29be1bf62fdf6cf2d6f4755a2c.png) jest największe i zwrócić
jest największe i zwrócić ![$ W[j][T] $](/files/tex/0d4cee4fc855224feaa789b6d8fc0da5d2113be9.png) jako wynik. Pozostaje pytanie, jak wyznaczyć tablice Q i W?
jako wynik. Pozostaje pytanie, jak wyznaczyć tablice Q i W?
Żeby to zrobić znowu trochę się pobawimy wzorami:
Załóżmy, że chcemy policzyć Q[j][n+1]. Ta wartość jest zdefiniowa jako maksimum z
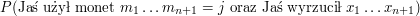 po wszystkich ciągach
po wszystkich ciągach 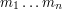 .
Przed chwilą pokazaliśmy, że jest to równe maksimum z
.
Przed chwilą pokazaliśmy, że jest to równe maksimum z
![$ P( \mbox{Jaś użył monet } m_1 \ldots m_n \mbox{oraz Jaś wyrzucił } x_1 \ldots x_{n} ) \cdot p[m_n][m_{n+1}] \cdot w[x_{n+1}][m_{n+1}] $](/files/tex/ada6bec16a9d548a364eca82dbdc17341a73bc34.png) po wszystkich ciągach
po wszystkich ciągach 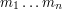 . Zauważmy, że:
. Zauważmy, że:
-
![$ w[x_{n+1}][m_{n+1}] = P( \mbox{Ja wyrzucił } x_{n+1} \mbox{ na monecie } m_{n+1} ) $](/files/tex/fe1fae64a35ddaecb1fbeeff66c337d05e07c8b2.png) zależy tylko od j
zależy tylko od j
-
![$ p[m_n][m_{n+1}] = %P( \mbox{Jaś użył w (n+1)-wszym rzucie monety } m_{n+1} \mbox{ | Jaś użył w n-tym rzucie monety } m_n) $](/files/tex/084ffdddba85d2173c5f2672baba659b5b048e15.png) zależy tylko od
zależy tylko od 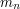 i
i 
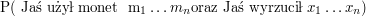 nie zależy od
nie zależy od  . Maksimum tego wyrażenia po
. Maksimum tego wyrażenia po 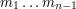 wynosi
wynosi
![$ Q[m_{n}][n] $](/files/tex/193d6be853961678faf2277fad85cecf2f139922.png)
Te trzy uwagi pozwalają nam zapisać ![$ Q[j][n+1] $](/files/tex/9beded3ddb0e3d5687f2f9a67eea346c452c9136.png) w nowy sposób. Otóż jest to maksimum z
w nowy sposób. Otóż jest to maksimum z ![$ Q[m_n][n] \cdot p[m_n][m_{n+1}] \cdot w[x_{n+1}][m_{n+1}] $](/files/tex/940ef394c2fe16094ccfb23a866526515ad6b22e.png) po wszystkich możliwych monetach
po wszystkich możliwych monetach 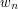 .
.



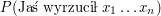 jest niezależny od ciągu monet. To oznacza, że ciąg monet, który maksymalizuje
jest niezależny od ciągu monet. To oznacza, że ciąg monet, który maksymalizuje 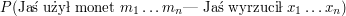 , maksymalizuje również
, maksymalizuje również 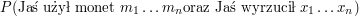 .
.


 razy i uzyskał wyniki
razy i uzyskał wyniki 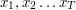 .
Jaki jest najbardziej prawdopodobny ciąg monet? Najprostszym sposobem, żeby go wyznaczyć jest następujący algorytm:
.
Jaki jest najbardziej prawdopodobny ciąg monet? Najprostszym sposobem, żeby go wyznaczyć jest następujący algorytm:
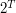 (mamy
(mamy  monet zamiast dwóch. Dane wejściowe tego algorytmu to:
monet zamiast dwóch. Dane wejściowe tego algorytmu to:
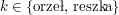 monetą
monetą  :
:
![$ w[i][k] = P( \mbox{ Jaś wyrzuci k} | \mbox{ Jaś rzuca monetą i} ) $](/files/tex/b9624b2a8e5113f2197905958fece6d0dab27205.png) ,
, , jeżeli w tej turze rzuca monetą
, jeżeli w tej turze rzuca monetą ![$ L[i][n] $](/files/tex/249450c06a1e1d1e6fd851d25fcef72a2c7186bc.png) będzie przechowywała najbardziej prawdopodobny ciąg monet
będzie przechowywała najbardziej prawdopodobny ciąg monet 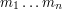 kończący się monetą
kończący się monetą 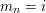 ).
Innymi słowy, chodzi o ciąg, który maksymalizuje prawdopodobieństwo
).
Innymi słowy, chodzi o ciąg, który maksymalizuje prawdopodobieństwo 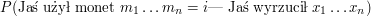 .
.
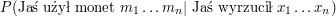
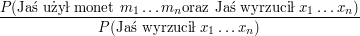
![$ Q[j][n] $](/files/tex/9d680455008a934b82638b64eec164bd1a7a6d73.png) będziemy przechowywali właśnie
będziemy przechowywali właśnie ![$ W[j][n] $](/files/tex/0a89f857bb812b242674267218a518369f434964.png) . Czyli maksymalizującym zarówno
. Czyli maksymalizującym zarówno
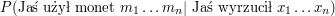 jak i
jak i 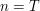 (liczba wszystkich rzutów monetą), to nasze zadanie będzie skończone.
Wystarczy wybrać to
(liczba wszystkich rzutów monetą), to nasze zadanie będzie skończone.
Wystarczy wybrać to ![$ Q[j][T] $](/files/tex/c5f2f4c4b2089b29be1bf62fdf6cf2d6f4755a2c.png) jest największe i zwrócić
jest największe i zwrócić ![$ W[j][T] $](/files/tex/0d4cee4fc855224feaa789b6d8fc0da5d2113be9.png) jako wynik. Pozostaje pytanie, jak wyznaczyć tablice Q i W?
jako wynik. Pozostaje pytanie, jak wyznaczyć tablice Q i W?
![$$
\begin{array}{rcl}
P( \mbox{Jaś użył monet } m_1 \ldots m_{n+1} \mbox{ oraz Jaś wyrzucił } x_1 \ldots x_{n+1}) & & = \\
P( \mbox{Jaś użył monet } m_1 \ldots m_n \mbox{oraz Jaś wyrzucił } x_1 \ldots x_{n} ) & \times & \\
P( \mbox{Jaś użył w (n+1)-wszym rzucie monety } m_{n+1} | \mbox{ Jaś użył w n-tym rzucie monety } m_n) & \times & \\
P( \mbox{Ja wyrzucił } x_{n+1} \mbox{ na monecie } m_{n+1} ) & & = \\
P( \mbox{Jaś użył monet } m_1 \ldots m_n \mbox{oraz Jaś wyrzucił } x_1 \ldots x_{n} ) \cdot p[m_n][m_{n+1}] \cdot w[x_{n+1}][m_{n+1}] & & \\
\end{array}
$$](/files/tex/f3942c87938e02b25e8f93460989eaaf1d351fa9.png)
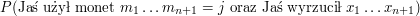 po wszystkich ciągach
po wszystkich ciągach ![$ P( \mbox{Jaś użył monet } m_1 \ldots m_n \mbox{oraz Jaś wyrzucił } x_1 \ldots x_{n} ) \cdot p[m_n][m_{n+1}] \cdot w[x_{n+1}][m_{n+1}] $](/files/tex/ada6bec16a9d548a364eca82dbdc17341a73bc34.png) po wszystkich ciągach
po wszystkich ciągach ![$ w[x_{n+1}][m_{n+1}] = P( \mbox{Ja wyrzucił } x_{n+1} \mbox{ na monecie } m_{n+1} ) $](/files/tex/fe1fae64a35ddaecb1fbeeff66c337d05e07c8b2.png) zależy tylko od j
zależy tylko od j![$ p[m_n][m_{n+1}] = %P( \mbox{Jaś użył w (n+1)-wszym rzucie monety } m_{n+1} \mbox{ | Jaś użył w n-tym rzucie monety } m_n) $](/files/tex/084ffdddba85d2173c5f2672baba659b5b048e15.png) zależy tylko od
zależy tylko od 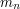 i
i 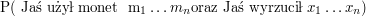 nie zależy od
nie zależy od 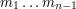 wynosi
wynosi
![$ Q[m_{n}][n] $](/files/tex/193d6be853961678faf2277fad85cecf2f139922.png)
![$ Q[j][n+1] $](/files/tex/9beded3ddb0e3d5687f2f9a67eea346c452c9136.png) w nowy sposób. Otóż jest to maksimum z
w nowy sposób. Otóż jest to maksimum z ![$ Q[m_n][n] \cdot p[m_n][m_{n+1}] \cdot w[x_{n+1}][m_{n+1}] $](/files/tex/940ef394c2fe16094ccfb23a866526515ad6b22e.png) po wszystkich możliwych monetach
po wszystkich możliwych monetach 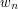 .
.


