Prawdopodobieństwo warunkowe i algorytm, który zadziwi Twoją panią od polskiego
15.06.2010 - Krzysztof Dryś
   Rzuty monetą dla średnio-zaawansowanychSpróbujmy czegoś trudniejszego. Jaś znowu będzie rzucał monetą. Tylko, że tym razem będzie ją zmieniał co jeden rzut. Innymi słowy, po każdym rzucie będzie losował, czy następnym razem będzie rzucał tą samą monetą, czy inną. Żeby łatwiej było nam to zrozumieć, zapiszmy całość jako algorytm:
Dane wejściowego tego algorytmu, to:
Nasz model się zmienił. Teraz Jaś może zmienić monetę po każdym rzucie. Teraz spróbujemy odpowiedzieć na następujące pytania:
Zacznijmy od pierwszego pytania. Niech
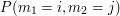 . Można to wyznaczyć jako: . Można to wyznaczyć jako:
 . .
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


![$ p[i,j] $](/files/tex/a37ca02be170344dc94955d0dedda83f499c4ece.png) określa prawdopodobieństwo tego, że w następnej turze Jaś będzie korzystał z monety
określa prawdopodobieństwo tego, że w następnej turze Jaś będzie korzystał z monety  pod warunkiem tego, że teraz korzysta z monety
pod warunkiem tego, że teraz korzysta z monety 
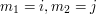 , oznacza że najpierw Jaś skorzystał z monety
, oznacza że najpierw Jaś skorzystał z monety 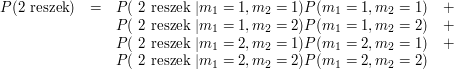
![$$P(m_1 = i, m_2 = j) = P(m_1 = i) \cdot P(m_2 = j | m_1 = i) = P(m_1 = i) p[i,j]$$](/files/tex/06c5034c24a8a83f26360e0ad9a31c929509eccb.png)
![$$
\begin{array}{rclc}
P(\mbox{2 reszek}) & = & P( \mbox{ 2 reszek } | m_1=1, m_2=1) P(m_1 = 1) p[1,1] &+\\
& & P( \mbox{ 2 reszek } | m_1=1, m_2=2) P(m_1 = 1) p[1,2] &+\\
& & P( \mbox{ 2 reszek } | m_1=2, m_2=1) P(m_1 = 2) p[2,1] &+\\
& & P( \mbox{ 2 reszek } | m_1=2, m_2=2) P(m_1 = 2) p[2,2] &\\
\end{array}
$$](/files/tex/37f47c3fa209e77bc07ed8123b13770ecdf3bc99.png)


