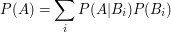Prawdopodobieństwo warunkowe i algorytm, który zadziwi Twoją panią od polskiego
15.06.2010 - Krzysztof Dryś
   Jak działa artykuł z poprzedniej strony? Żeby odpowiedzieć sobie na to pytanie musimy dowiedzieć się paru rzeczy o prawdopodobieństwie. Wyobraźmy sobie, że mamy idealna kostkę 6-ścienną. Jakie jest prawdopodobieństwo, że rzucając nią wyrzucimy jedynkę, dwójkę lub trójkę? To proste:
Spróbujmy czegoś trochę trudniejszego. Wyobraźmy sobie, że rzuciliśmy kostką i poprosiliśmy naszego kolegę Jasia, żeby odczytał za nas wynik. Jaś to dobry chłopak, tylko trochę złośliwy. Dlatego zdecydował, że nie powie nam, co wypadło. Zamiast tego, wyjawił nam, że wypadła liczba nieparzysta. Jakie teraz jest prawdopodobieństwo, że wypadła jedynka, dwójka lub trójka?
Prawdopodobieństwo warunkowe opisuje właśnie prawdopodobieństwo zajścia zdarzenia A pod warunkiem zajścia zdarzenia B. W naszym przykładzie:
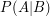 . Można je policzyć w bardzo prosty sposób: . Można je policzyć w bardzo prosty sposób:
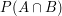 oznacza prawdopodobieństwo tego, że zaszło zdarzenie A
oraz zdarzenie B. W naszym wypadku: oznacza prawdopodobieństwo tego, że zaszło zdarzenie A
oraz zdarzenie B. W naszym wypadku:
Popatrzmy na jeszcze jedną ciekawą cechę prawdopodobieństwa warunkowego. Niech
zdarzenia
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


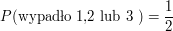

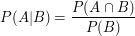
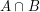 = wypadło 1,2 lub 3 oraz wypadła liczba nieparzysta = wypadło 1 lub 3
= wypadło 1,2 lub 3 oraz wypadła liczba nieparzysta = wypadło 1 lub 3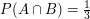
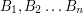 będą takie, że:
będą takie, że:
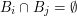 , dla
, dla 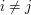 , to znaczy te zbiory są rozłączne,
, to znaczy te zbiory są rozłączne,
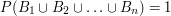 , to znaczy - zawsze musi zajść przynajmniej jedno z nich.
, to znaczy - zawsze musi zajść przynajmniej jedno z nich.