Ślepe podpisy cyfrowe
Ślepe podpisy cyfrowe to drugi, obok zobowiązania bitowego mechanizm, który zostanie wykorzystany do pokazania, jak można zaprojektować pieniądze cyfrowe, tak aby posiadały własności przydatne w procesie dokonywania transakcji. Aby podpis był ślepy, musi spełniać kilka wymagań:
- Po pierwsze, Alicja przygotowując dokument do podpisu, nie powinna być w stanie sama go podpisać (ani nikt inny, jeśli podpis przynależy do Boba).
- Alicja musi umieć przygotować do podpisu dokument w taki sposób, aby Bob po otrzymaniu dokumentu mógł wygenerować pod nim podpis nie poznając treści dokumentu. Można to sobie wyobrażać jako zamkniętą kopertę, z dokumentem w środku, wysyłaną do Boba. W kopercie umieszczona jest kalka, pozwalająca skopiować na kartkę dokumentu to, co napisze na niej Bob.
- Nieautoryzowany dostęp do zawartości koperty powinien być niemożliwy. Można myśleć, że koperta powinna ulec samospaleniu, jeśli Bob spróbuje ją otworzyć. Oczywiście w cyfrowym świecie nie potrzebujemy samospalających się kopert, ponieważ dysponujemy technikami kryptograficznymi -- użyjemy tutaj szyfrowanie z zaślepianiem, które praktycznie uniemożliwia nieautoryzowane otwarcie koperty.
- Przed podpisaniem Bob powinien wiedzieć, że to co podpisuje pochodzi od Alicji.
-
Alicja natomiast powinna umieć otworzyć kopertę bez żadnych niespodzianek, wymagających użycia gaśnicy.
-
Jeśli będzie chciała kiedyś pokazać Bobowi kartkę niezapakowaną, Bob musi umieć stwierdzić, czy dokument był podpisany przez niego.
-
Dodatkowo, jeśli Alicja z pewnych powodów musiałaby pokazać Bobowi kopię dokumentu, Bob powinien posiadać umiejętność weryfikacji, czy koperta którą otrzymał wcześniej od Alicji zawierała kopię tego dokumentu, czy nie.
W świecie cyfrowym wszystkie te własności posiada schemat podpisu wymyślony przez Davida Chauma. Dokument to po prostu ciąg bitów, koperta odpowiada szyfrowaniu z zaślepianiem. Zainteresowany czytelnik może przeczytać o tym w artykule Agaty Murawskiej "Nie wiesz, co podpisujesz – protokoły ślepych podpisów".
Dla naszych potrzeb wprowadzimy oznaczenia mechanizmów opisanych dokładniej we wspomnianym artykule:
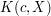 – dokument
– dokument  umieszczony w kopercie
umieszczony w kopercie 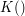 z dodatkowym elementem
z dodatkowym elementem  ,
,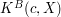 – koperta podpisana przez Boba,
– koperta podpisana przez Boba,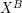 – dokument z podisem Boba (już bez koperty),
– dokument z podisem Boba (już bez koperty),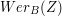 – procedura weryfikująca podpis Boba na dokumencie
– procedura weryfikująca podpis Boba na dokumencie 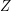 , która odpowiada
, która odpowiada 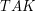 wtedy, gdy podpis został złożony ręką Boba, w przeciwnym przypadku
wtedy, gdy podpis został złożony ręką Boba, w przeciwnym przypadku 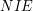 .
.
Element  będzie mieć znaczenie, gdy Alicja będzie chciała przekonać Boba, że dokument
będzie mieć znaczenie, gdy Alicja będzie chciała przekonać Boba, że dokument  jest w
jest w 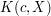 . Przed weryfikacją Alicja podaje
. Przed weryfikacją Alicja podaje  i
i  , a Bob sprawdza. Bez
, a Bob sprawdza. Bez  Bob nie jest w stanie niczego stwierdzić.
Bob nie jest w stanie niczego stwierdzić.
Aby przybliżyć znaczenie symboli zawartych w napisie 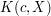 , opiszemy jak koperta
, opiszemy jak koperta 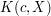 jest zrealizowana na poziomie kryptograficznym. Otóż
jest zrealizowana na poziomie kryptograficznym. Otóż 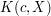 jest równe liczbie
jest równe liczbie
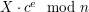 . Para
. Para 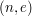 jest kluczem publicznym Boba dla szyfrowania RSA.
jest kluczem publicznym Boba dla szyfrowania RSA.  to liczba służąca zaciemnieniu dokumentu
to liczba służąca zaciemnieniu dokumentu  , który w świecie kryptografii interpretowany jest jako liczba naturalna.
, który w świecie kryptografii interpretowany jest jako liczba naturalna.
Załóżmy, że Bob otrzymał w chwili 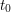 liczbę
liczbę 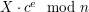 . Kiedy Bob zechce sprawdzić zawartość koperty w chwili
. Kiedy Bob zechce sprawdzić zawartość koperty w chwili 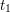 późniejszej od
późniejszej od 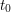 , może popoprosić Alicję o ujawnienie zawartości koperty. Alicja prześle mu wtedy parę
, może popoprosić Alicję o ujawnienie zawartości koperty. Alicja prześle mu wtedy parę 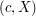 .
Bob potrafi sprawdzić czy liczba przysłana przez Alicję w chwili
.
Bob potrafi sprawdzić czy liczba przysłana przez Alicję w chwili 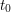 jest równa
jest równa 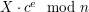 . Bob potrafi wykonać szybko takie obliczenia gdyż umie mnożyć, podnosić do potęgi oraz zna
. Bob potrafi wykonać szybko takie obliczenia gdyż umie mnożyć, podnosić do potęgi oraz zna  i
i  (bo są to składowe jego klucza publicznego). Alicja natomiast ma niewielkie szanse oszukania Boba. Mogłaby wysłać Bobowi inny dokument
(bo są to składowe jego klucza publicznego). Alicja natomiast ma niewielkie szanse oszukania Boba. Mogłaby wysłać Bobowi inny dokument 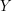 ale wtedy musiałaby obliczyć
ale wtedy musiałaby obliczyć 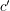 , które jest tekstem jawnym dla szyfrogramu
, które jest tekstem jawnym dla szyfrogramu 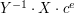 . Znalezienie takiego
. Znalezienie takiego 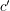 jest równoważne ze złamaniem RSA co uznaje się za trudne w praktyce.
jest równoważne ze złamaniem RSA co uznaje się za trudne w praktyce.





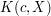 – dokument
– dokument  umieszczony w kopercie
umieszczony w kopercie 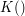 z dodatkowym elementem
z dodatkowym elementem  ,
,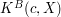 – koperta podpisana przez Boba,
– koperta podpisana przez Boba,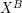 – dokument z podisem Boba (już bez koperty),
– dokument z podisem Boba (już bez koperty),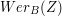 – procedura weryfikująca podpis Boba na dokumencie
– procedura weryfikująca podpis Boba na dokumencie 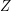 , która odpowiada
, która odpowiada 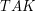 wtedy, gdy podpis został złożony ręką Boba, w przeciwnym przypadku
wtedy, gdy podpis został złożony ręką Boba, w przeciwnym przypadku 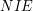 .
.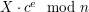 . Para
. Para 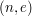 jest kluczem publicznym Boba dla szyfrowania RSA.
jest kluczem publicznym Boba dla szyfrowania RSA. 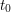 liczbę
liczbę 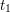 późniejszej od
późniejszej od 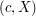 .
Bob potrafi sprawdzić czy liczba przysłana przez Alicję w chwili
.
Bob potrafi sprawdzić czy liczba przysłana przez Alicję w chwili  i
i  (bo są to składowe jego klucza publicznego). Alicja natomiast ma niewielkie szanse oszukania Boba. Mogłaby wysłać Bobowi inny dokument
(bo są to składowe jego klucza publicznego). Alicja natomiast ma niewielkie szanse oszukania Boba. Mogłaby wysłać Bobowi inny dokument 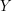 ale wtedy musiałaby obliczyć
ale wtedy musiałaby obliczyć 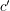 , które jest tekstem jawnym dla szyfrogramu
, które jest tekstem jawnym dla szyfrogramu 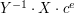 . Znalezienie takiego
. Znalezienie takiego 

