Ponownie odwiedziny u RSA
 David Chaum
David Chaum jest pomysłodawcą i twórcą pierwszych protokołów dla ślepych podpisów i elektronicznych pieniędzy. Przyczynił się także do powstania pierwszych sieci anonimowych.
RSA jest jednym z najlepiej opisanych i zbadanych algorytmów w kryptografii. Nic zatem dziwnego, że podstawowy protokół ślepego podpisu będzie oparty właśnie na podpisach RSA. Autorem poniższego schematu jest pomysłodawca ślepych podpisów,
David Chaum.
Kolejne kroki schematu opisanego w poprzedniej części są realizowane w następujący sposób:
1. (Generowanie klucza) Podpisujący generuje klucz publiczny RSA 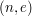 oraz klucz prywatny
oraz klucz prywatny 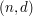
2. (Zaciemnianie) Zaciemniający wybiera dla danej wiadomości  pewną losową liczbę
pewną losową liczbę  , taką, że
, taką, że 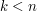 i
i  względnie pierwsze z
względnie pierwsze z  . Następnie oblicza zaciemnienie
. Następnie oblicza zaciemnienie 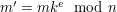 i wysyła
i wysyła 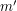 jako wiadomość do podpisu.
jako wiadomość do podpisu.
3. (Generowanie podpisu) Podpisujący oblicza 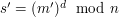 jako podpis pod wiadomością
jako podpis pod wiadomością 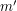 i wysyła
i wysyła 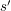 do zaciemniającego.
do zaciemniającego.
4. (Zdejmowanie zaciemnienia) Zaciemniający oblicza (przy pomocy rozszerzonego alg. Euklidesa) 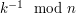 , a następnie odtwarza podpis pod niezaciemnioną wiadomością:
, a następnie odtwarza podpis pod niezaciemnioną wiadomością:
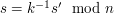
5. (Weryfikacja podpisu) Mając wiadomość  , podpis
, podpis  i klucz
i klucz 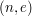 podpisującego, sprawdza się, jak przy zwykłym podpisie cyfrowym, czy
podpisującego, sprawdza się, jak przy zwykłym podpisie cyfrowym, czy 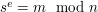
Dlaczego to działa?
Policzmy, że faktycznie podpisanie wiadomości

nieznanym nam kluczem
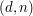
daje w efekcie podpis

:
Zgadza się!
Poświęćmy jeszcze chwilę na analizę przedstawionego schematu. Przede wszystkim, interesują nas odpowiedzi na trzy pytania:
Czy podpisujący może poznać tożsamość zaciemniającego podczas weryfikacji?
Wiemy, że podpisujący zna tożsamość autora wiadomości podczas jej podpisywania. Czy może w jakiś sposób wykorzystać te informacje, żeby skojarzyć wiadomość  z jej zaciemnioną wersją
z jej zaciemnioną wersją 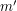 ?
?
Wszystko, co dzieje się podczas podpisywania, może być zapisywane przed składającego podpis - załóżmy zatem, że ma on bazę zaciemnionych wiadomości i podpisów (czyli trójek 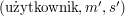 ).
).
Czy dostając wiadomość  i podpis
i podpis  może coś powiedzieć o
może coś powiedzieć o 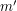 ?
?
-
Jak było wygenerowane
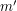 , zaciemniona wiadomość powstała z
, zaciemniona wiadomość powstała z  ?
?
Do jego stworzenia użyliśmy jakiejś losowej liczby  , o której podpisujący nic nie wie - zatem odtworzenie
, o której podpisujący nic nie wie - zatem odtworzenie 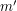 na podstawie
na podstawie  nie jest możliwe.
nie jest możliwe.
-
Może zatem uda się odzyskać podpis
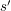 i znaleźć pasującą trójkę w bazie?
i znaleźć pasującą trójkę w bazie?
Też nie - skoro 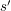 powstaje przez podpisanie
powstaje przez podpisanie 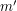 , to nie odzyskamy go bez wiedzy o zaciemnionej wiadomości, wysłanej do podpisu.
, to nie odzyskamy go bez wiedzy o zaciemnionej wiadomości, wysłanej do podpisu.
Jesteśmy zatem bezpieczni - nie da się, nie znając naszych wszystkich sekretów, powiązać zaciemnionej i niezaciemnionej wiadomości.
Czy spełnione są warunki dotyczące bezpiecznego ślepego podpisu?
Problem może wystąpić, jeśli uda się znaleźć takie 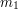 i
i 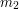 , które przemnożone odpowiednio przez
, które przemnożone odpowiednio przez 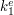 i
i 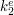 dają tę samą zaciemnioną wiadomość
dają tę samą zaciemnioną wiadomość 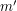 . Wówczas uzyskanie podpisu dla jednej z tych wiadomości, umożliwia posługiwanie się obiema. Na szczęście, znalezienie dla ustalonej wiadomości
. Wówczas uzyskanie podpisu dla jednej z tych wiadomości, umożliwia posługiwanie się obiema. Na szczęście, znalezienie dla ustalonej wiadomości 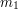 pasującego
pasującego 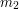 jest obliczeniowo bardzo trudne.
jest obliczeniowo bardzo trudne.
Czy można do podpisów ślepych używać tej samej pary kluczy, co do szyfrowania wiadomości?
Możliwe zagrożenie ilustruje poniższy obrazek:

Bob wysyła do Notariusza bardzo ważny i tajny dokument  , zaszyfrowany kluczem publicznym Notariusza,
, zaszyfrowany kluczem publicznym Notariusza, 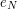 . Annie udaje się przechwycić ten dokument, zatem zaciemnia go i wysyła do podpisu Notariuszowi, który w dobrej wierze podpisuje i odsyła do Anny. Co tu się dzieje?
. Annie udaje się przechwycić ten dokument, zatem zaciemnia go i wysyła do podpisu Notariuszowi, który w dobrej wierze podpisuje i odsyła do Anny. Co tu się dzieje?
Anna przechwyciła wiadomość 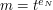 , przemnożyła przez pewne
, przemnożyła przez pewne 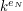 i wysłała do Notariusza. Notariusz podpisał całość i odesłał, zatem Anna otrzymała wiadomość
i wysłała do Notariusza. Notariusz podpisał całość i odesłał, zatem Anna otrzymała wiadomość 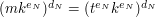 . Teraz wystarczy, że obliczy podpis dla wiadomości
. Teraz wystarczy, że obliczy podpis dla wiadomości 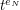 - będzie to, jak widać,
- będzie to, jak widać, 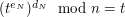 . Notariusz nie miał szansy zauważyć, że odszyfrował dla Anny wiadomość nieprzeznaczoną dla niej, gdyż była ona zaciemniona!
. Notariusz nie miał szansy zauważyć, że odszyfrował dla Anny wiadomość nieprzeznaczoną dla niej, gdyż była ona zaciemniona!
Z drugiej strony, Anna może po prostu wysłać korzystną dla niej, zaciemnioną wiadomość do podpisu - ot, na przykład, "Ja, Notariusz, zrzekam się całego mojego majątku na rzecz Anny". Po zaciemnieniu wiadomość będzie nieczytelna i niewzbudzająca podejrzeń, zostanie więc podpisana - Anna będzie wówczas dysponowała pismem "od Notariusza" (no przecież je podpisał!), w którym zrzeka się on majątku na rzecz Anny. Nic, tylko wyegzekwować wykonanie!
Widzimy więc, że pod żadnym pozorem nie można używać tej samej pary kluczy do protokołu ślepych podpisów i szyfrowania.



 nieznanym nam kluczem
nieznanym nam kluczem 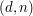 daje w efekcie podpis
daje w efekcie podpis  :
: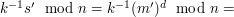
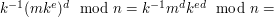
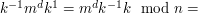
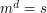


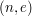 oraz klucz prywatny
oraz klucz prywatny 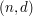
 , taką, że
, taką, że 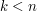 i
i  . Następnie oblicza zaciemnienie
. Następnie oblicza zaciemnienie 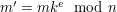 i wysyła
i wysyła 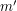 jako wiadomość do podpisu.
jako wiadomość do podpisu.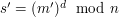 jako podpis pod wiadomością
jako podpis pod wiadomością 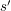 do zaciemniającego.
do zaciemniającego.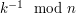 , a następnie odtwarza podpis pod niezaciemnioną wiadomością:
, a następnie odtwarza podpis pod niezaciemnioną wiadomością: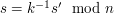
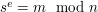
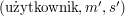 ).
).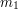 i
i 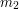 , które przemnożone odpowiednio przez
, które przemnożone odpowiednio przez 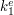 i
i 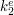 dają tę samą zaciemnioną wiadomość
dają tę samą zaciemnioną wiadomość 
 , zaszyfrowany kluczem publicznym Notariusza,
, zaszyfrowany kluczem publicznym Notariusza, 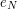 . Annie udaje się przechwycić ten dokument, zatem zaciemnia go i wysyła do podpisu Notariuszowi, który w dobrej wierze podpisuje i odsyła do Anny. Co tu się dzieje?
. Annie udaje się przechwycić ten dokument, zatem zaciemnia go i wysyła do podpisu Notariuszowi, który w dobrej wierze podpisuje i odsyła do Anny. Co tu się dzieje?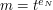 , przemnożyła przez pewne
, przemnożyła przez pewne 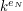 i wysłała do Notariusza. Notariusz podpisał całość i odesłał, zatem Anna otrzymała wiadomość
i wysłała do Notariusza. Notariusz podpisał całość i odesłał, zatem Anna otrzymała wiadomość 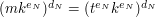 . Teraz wystarczy, że obliczy podpis dla wiadomości
. Teraz wystarczy, że obliczy podpis dla wiadomości 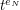 - będzie to, jak widać,
- będzie to, jak widać, 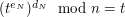 . Notariusz nie miał szansy zauważyć, że odszyfrował dla Anny wiadomość nieprzeznaczoną dla niej, gdyż była ona zaciemniona!
. Notariusz nie miał szansy zauważyć, że odszyfrował dla Anny wiadomość nieprzeznaczoną dla niej, gdyż była ona zaciemniona!

