Proste przetwarzanie obrazów
23.12.2009 - Rafał Kozik
  2. Operacje per-pixelZabawę z przetwarzaniem obrazów zaczniemy od filtrów, które będą wykonywały operacje dla każdego piksela z osobna. Dla uproszczenia będziemy zajmować się kolorami w postaci RGB, mimo, że w niektórych przypadkach wygodniej byłoby użyć HSV. Będziemy operować na wartościach r, g i b (oznaczających odpowiednie składowe). Zakładamy też, że po wykonaniu każdej operacji wartości te zostaną przycięte do przedziału [0; 255] (wartości ujemne zastąpimy przez 0, a dodatnie wartości spoza zakresu zamienimy na 255). Wybór składowejJeżeli chcemy zobaczyć jak wygląda któraś składowa obrazu (czerwona, zielona, niebieska), możemy po prostu ustawić pozostałe wartości na 0. Dla naszego obrazu testowego wygląda to tak:  Nie jest to nic nadzwyczajnego, ale pozwala nam lepiej zrozumieć w jaki sposób został zbudowany obraz, który widzimy.
InwersjaJednym z typowych efektów jest negatyw. Myślę, że z aktualną wiedzą nie stanowiłoby już problemu napisanie odpowiedniej operacji, która pozwoliłaby na wygenerowanie takiego obrazu:  Barwę każdego piksela musimy zamienić na barwę dopełniającą. Gdyby 'dodać' do siebie obraz i jego negatyw, otrzymalibyśmy w wyniku obraz całkowicie biały.
Odcienie szarościKiedyś, dawno temu, królowały zdjęcia czarno białe. Teraz, poprzewracało nam się w głowach od ogromu dostępnych kolorów i czasami chcemy, żeby powróciły tamte prostsze czasy. A poważniej, niektóre zdjęcia po prostu wyglądają lepiej w odcieniach szarości, pozwala to na dodanie im odpowiedniego nastroju:  Zmiana na odcienie szarości jest trochę bardziej skomplikowana niż poprzednie filtry i aby ją wykonać, musimy zorientować się w jaki sposób działa ludzie oko. Ponieważ nie rozpoznajemy każdej składowej z taką samą intensywnością, powinny one mieć różny wpływ na obraz wynikowy (różne ilości czopków rozpoznających odpowiednie barwy). Na szczęście takie dane łatwo dziś w Internecie znaleźć. Zatem po chwilowych poszukiwaniach wiemy już, że 29.9% będzie stanowić składowa czerwona, 58.7% zielona i 11.4% niebieska. Gotowy filtr ma następującą postać:
JasnośćKolejnym prostym filtrem, który chcę pokazać jest zmiana jasności. Zastanówmy się przez chwilę co to znaczy, że chcemy rozjaśnić jakiś obraz. Chcemy, żeby każdy z pikseli stał się bliższy bieli. A co to znaczy przyciemnić obraz? Każdy piksel powinien stać się bliższy czerni. Idąc dalej tym rozumowaniem dochodzimy do wniosku, że wystarczy składowe każdego piksela zmodyfikować o pewną wartość. Przykładowo, gdy zwiększymy je o 100, otrzymamy taki rezultat: 
KontrastPomysł na zmianę kontrast jest dość ciekawy. Zwiększając kontrast chcemy, żeby ciemne piksele stały się jeszcze ciemniejsze, a jasne jaśniejsze. Jeżeli od każdej składowej odejmiemy 128, to dostaniemy wtedy wartość z zakresu [-128; 127]. Ciemne kolory będą miały ujemne wartości, a jasne dodatnie. Jeżeli przemnożymy to przez jakąś liczbę większą od 1 to wartości składowych ciemnych kolorów zmaleją, a jasnych urosną. Na koniec wystarczy dodać 128, żeby wrócić do odpowiedniego zakresu. Gdy pomnożymy przez 8, otrzymamy taki wynik: 
GammaOstatnim filtrem, o którym tutaj wspomnę, jest filtr gamma. Korekcja gamma jest nieliniową operacją przekształcającą dane, która opisana jest wzorem (gamma jest grecką literą uzytą w wykładniku): 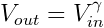 Niektóre urządzenia, jak np. monitory, skanery wprowadzają pewne zakłócenia przez to, że ich sposób podświetlania nie jest idealny. Chodzi o to, że jeżeli moc światła będzie ustawiona na 50%, to wcale nie oznacza, że będzie świecić w połowie tego co gdy moc ustawiona jest na 100%. Bardzo dobrze obrazuje to ten wykres z wikipedii: 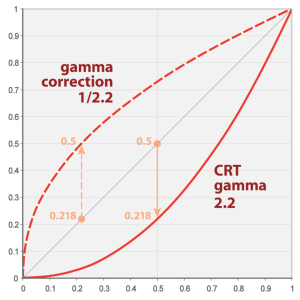 Zatem moc przekłada się na jasność zgodnie z takim wzorem (powyżej gamma była równa 2.2): 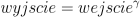 Dolna krzywa pokazuje jak przykładowo wzrasta jasność wraz z mocą dla monitora kineskopowego. Ponieważ chcemy zobaczyć obraz taki jaki jest naprawdę, robimy prostą operację matematyczną, która sprawi, że obraz na monitorze będzie wyglądał tak jak powinien. A dokładniej chcemy zrobić coś takiego: 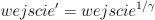 Gdy teraz będziemy chcieli wyświetlić tak przetworzony obraz, na wyjściu dostaniemy: 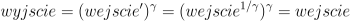 Dla gamma równego 2.2 dostaniemy taki, jaśniejszy obraz: 
3. Operacje per-pixel -- apletSkoro już wiemy w jaki sposób wykonywane są operacje per-pixel, możemy z tym chwilę poeksperymentować. Poniższy aplet ma wbudowane wszystkie filtry, które zostały pokazane powyżej, pozwala też na pisanie własnych. Operacje są pisane w języku JavaScript (można używać biblioteki matematycznej). Zgłoś problem z apletem (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




