Permutacje
18.11.2009 - Marcin Oczeretko
 Gorąco zachęcam do zmierzenia się z dwoma prostymi problemami programistycznymi. Wszystkie potrzebne do ich rozwiązania informacje znajdują się w artykule, choć możliwe, że zadania te będą mimo to wymagały chwili zastanowienia. Poprawność swoich programów możecie zbadać, wysyłając je na sprawdzaczkę. Cykle Dla danej permutacji P określonej na zbiorze
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Po kolei Wiemy już, że wszystkich permutacji zbioru
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(9 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


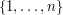 wyznacz długość najdłuższego cyklu występującego w jej rozkładzie na cykle.
wyznacz długość najdłuższego cyklu występującego w jej rozkładzie na cykle.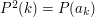 i
i 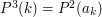 .
. (
(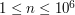 ) z treści zadania.
) z treści zadania.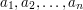 , (
, (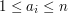 ), które definiują permutację
), które definiują permutację  w następujący sposób:
w następujący sposób: 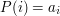 .
.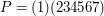
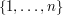 jest
jest 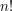 . Dla danego
. Dla danego 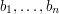 opisują permutacje
opisują permutacje  i
i  , to
, to  , że:
, że: 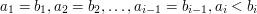 ).
).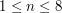 ).
).

