Krowa, las i eksploracja terenu
17.11.2009 - Marcin Bieńkowski
   Czy naprawdę trzeba tyle chodzić?Krótka odpowiedź brzmi: tak, każdy algorytm dla krowy wymaga przejścia w
najgorszym przypadku odległości dziewięciokrotnie przekraczającej początkową
odległość krowy od pastwiska. Niestety pokazanie tego jest dość trudne i
wykracza poza ramy tego artykułu. Spróbujmy jednak uspokoić swoje sumienie i
pokazać, że krowa zawsze musi przejść co najmniej
Zauważmy teraz, że krowa stosuje taką samą trasę niezależnie od tego jaki
jest X. Powyższe zdanie wydaje się oczywiste (jak trasa mogłaby od
tego zależeć, skoro X poznajemy dopiero w momencie odnalezienia
pastwiska, a wtedy już nigdzie nie lazimy), ale je warto przeczytać więcej niż
jeden raz. Oznacza to, że dla danego wyboru trasy krowy (tj. liczb Popatrzmy bliżej na ciąg
Wtedy krowa przechodzi co najmniej
Ponieważ Po co krowie pieniądze?Jak można ułatwić życie naszej krowie? Na początku poprzedniego rozdziału powiedzieliśmy, że nie da się poprawić wyniku osiąganego przez algorytm Smart-Cow. Cóż, jest to tylko częściowa prawda. Nie można go poprawić, jeśli krowa chodzi deterministycznie. Możemy natomiast podarować jej monetę, którą może wspomóc się w w trudnych chwilach (i nie chodzi nam o to, żeby kupiła sobie za to mapę czy coś do jedzenia). Wróćmy do algorytmu
Smart-Cow. Załóżmy, że w momencie, który nazwaliśmy krytycznym, krowa rzuca
monetą. Jeśli wypadnie orzeł idzie następne
To obniża średnią liczbę metrów przebytą przez krowę, pod warunkiem że ... krowa wymyśli, że dany moment jest krytyczny! Okazuje się jednak, że wcale nie musi tego robić. Wystarczy, żeby monetą rzuciła wybierając kierunek na samym początku. Wtedy analiza jest dokładnie taka sama, a dodatkowo w momencie kiedy krowa znajdzie się już w punkcie krytycznym z prawdopodobieństwem 1/2 będzie szła w lewo a z prawdopodobieństwem 1/2 będzie szła w prawo. Quo vadis, droga krowoPowyższe rozważania to tylko czubek góry lodowej tematyki eksploracji terenu. Oprócz ,,prawdziwych'' zastosowań, istnieje jeszcze parę lepiej lub gorzej zbadanych podstawowych problemów. Przykładowo dociekliwy czytelnik może zastanowić się jaką strategię należy obrać, jeśli jesteśmy kapitanem, który odpłynął od brzegu i stracił orientację. Zakładamy, że linia brzegowa jest linią prostą i chcemy dopłynąć do jej dowolnego miejsca. Można wyobrazić sobie następujące warianty tego problemu:
Temperować ołówki, siodłać krowy i do dzieła! (14 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


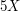 .
. 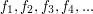 , gdzie
, gdzie 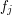 jest oddaleniem w
fazie j. (W opisanym wcześniej algorytmie Smart-Cow
jest oddaleniem w
fazie j. (W opisanym wcześniej algorytmie Smart-Cow 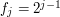 .)
.)
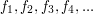 ) wystarcza postawić bramkę na pastwisko w jakimś bardzo
złośliwym miejscu.
) wystarcza postawić bramkę na pastwisko w jakimś bardzo
złośliwym miejscu.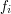 i
i 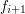 taka że
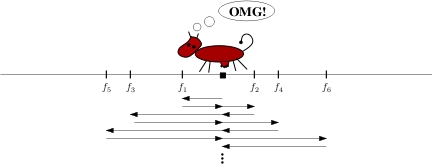
taka że 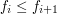 . Na powyższym rysunku
jest to na przykład para
. Na powyższym rysunku
jest to na przykład para 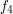 i
i 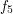 . W przeciwnym wypadku ciąg
. W przeciwnym wypadku ciąg 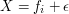 .
.
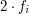 w lewo, następnie
w lewo, następnie 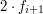 w prawo, a następnie (pod warunkiem, że nie jest bezdennie głupia i
w prawo, a następnie (pod warunkiem, że nie jest bezdennie głupia i
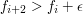 ) krowa dochodzi do pastwiska przechodząc
X. Całkowita droga przebyta przez krowę to
) krowa dochodzi do pastwiska przechodząc
X. Całkowita droga przebyta przez krowę to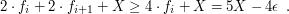
 możemy wybrać dowolnie małe i zaniedbywalne, krowa
przechodzi praktycznie pięciokrotnie więcej niż wynosi
możemy wybrać dowolnie małe i zaniedbywalne, krowa
przechodzi praktycznie pięciokrotnie więcej niż wynosi  .
.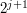 metrów w prawo, w
przeciwnym przypadku w lewo. Dla ustalonej pozycji bramki na pastwisko krowa ma
1/2 szansy na to, że pójdzie w jej stronę. W takim przypadku części spaceru
krowy (niebieski fragment na rysunku) o długości
metrów w prawo, w
przeciwnym przypadku w lewo. Dla ustalonej pozycji bramki na pastwisko krowa ma
1/2 szansy na to, że pójdzie w jej stronę. W takim przypadku części spaceru
krowy (niebieski fragment na rysunku) o długości 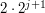 w ogóle nie
ma! Wtedy krowa przechodzi nie
w ogóle nie
ma! Wtedy krowa przechodzi nie 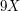 a
a 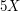 . W średnim przypadku przechodzi
zatem
. W średnim przypadku przechodzi
zatem 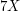 .
.