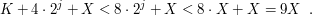Krowa, las i eksploracja terenu
17.11.2009 - Marcin Bieńkowski
   Łata na łacieTu mała dygresja: informatycy, jak i wszystkie umysły ścisłe uwielbiają: a) łatanie złych rozwiązań zamiast pisania ich od początku, b) redukcje. Do tego stopnia, że często wpadają w pułapki jak w opisana niżej historia (z długaśną brodą) o czajniku.
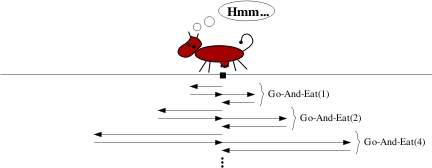
Zastanówmy się zatem, czy przez ,,łatanie'' algorytmu Go-And-Eat i dodanie punktu 4 nie postąpiliśmy przypadkiem jak prawdziwi informatycy (a nie chcielibyśmy tego robić, bo po co męczyć steraną życiem i mocno już wygłodniałą krowę). Zobaczmy, jak wygląda droga, po której teraz chodzi krowa.
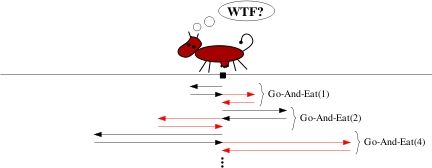
Może nie jest oczywiste, co można tutaj poprawić. Ale... pamiętacie, że to w którą stronę krowa zaczyna wykonywanie algorytmu Go-And-Eat nie ma znaczenia? W takim razie narysujmy drogę krowy która nieparzyste wykonania algorytmu Go-And-Eat zaczyna w stronę lewą a parzyste w prawą.
Bez sensu, prawda? Krowa idzie w jedną stronę Algorytm Smart-Cow
Spróbujmy teraz przeanalizować, jaki dystans pokona krowa w najgorszym
przypadku.Weźmy takie naturalne j, że zachodzi
Nazwijmy ten punkt krytycznym, przyda się on w dalszej części
artykułu. Następnie krowa chce iść
(14 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


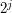 metrów, tylko po to żeby
wrócić do punktu wyjścia i pójść w tę samą stronę
metrów, tylko po to żeby
wrócić do punktu wyjścia i pójść w tę samą stronę 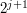 metrów!
Wyrzućmy zatem nadmiarowe spacery (zaznaczone na czerwono na rysunku powyżej).
Zmodyfikowany algorytm prezentuje się następująco:
metrów!
Wyrzućmy zatem nadmiarowe spacery (zaznaczone na czerwono na rysunku powyżej).
Zmodyfikowany algorytm prezentuje się następująco: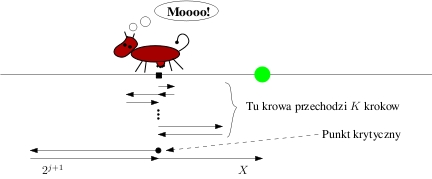
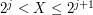 .
Oznacza to, że pierwsze j wykonań pętli w punkcie 3 powyższego
algorytmu (z wartościami
.
Oznacza to, że pierwsze j wykonań pętli w punkcie 3 powyższego
algorytmu (z wartościami 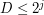 ) nie spowoduje znalezienia pastwiska.
Droga w metrach przebyta przez krowę do tego momentu wynosi
) nie spowoduje znalezienia pastwiska.
Droga w metrach przebyta przez krowę do tego momentu wynosi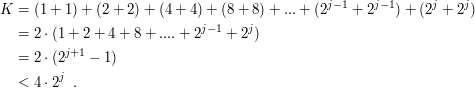
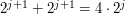 metrów. Następnie krowa zamierza iść
metrów. Następnie krowa zamierza iść 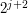 metrów, ale już po
X metrach napotyka pastwisko. Sumarycznie jej całkowita droga to
co najwyżej
metrów, ale już po
X metrach napotyka pastwisko. Sumarycznie jej całkowita droga to
co najwyżej