Algorytm Euklidesa
31.10.2009 - Damian Rusak
 ZadaniaZastanów się nad dwoma poniższymi problemami (możesz wysłać do nich rozwiązanie na sprawdzaczkę). 1. Mamy liczbę pierwszą 2. Rozważmy wspominany problem aptekarza, z jednym dodatkiem - aptekarz chciałby użyć jak najmniej odważników. Jak znaleźć takie rozwiązanie? Poniżej znajdują się dokładne specyfikacje tych zadań i okienka do wysłania rozwiązań. Zachęcamy do spróbowania swoich sił!
Zadanie MonetyLimit czasowy: 1s; Limit pamięciowy: 16 MB Aptekarz Joe bardzo lubi liczyć bilon z kasy w swojej aptece. Dzisiaj wpadł na pomysł, aby wziąć sobie dwie monety o pewnych nominałach i znaleźć taką kwotę, którą można wypłacić zarówno za pomocą dowolnej ilości monet pierwszego rodzaju jak i za pomocą dowolnej ilości monet drugiego rodzaju. Joe nie jest zbyt inteligentny, poprosił więc Cię o pomoc. Napisz program, który znajdzie dla niego taką kwotę! Wejście: Pierwsza linia wejścia składa się z jednej liczby całkowitej Wyjście: Dla każdej pary należy na wyjściu wypisać jedną linię z jedną liczbą - najmniejszą taką kwotą, którą można wypłacić zarówno za pomocą nominału Przykład: Dla wejścia: 3 Poprawne wyjście to: 30 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
OdwrotnośćLimit czasowy: 1s; Limit pamięciowy: 16MB Liczby pierwsze mają bardzo dużo ciekawych właściwości. Jedną z nich jest to, że każda liczba całkowita, mniejsza od danej liczby pierwszej, ma swoją unikalną odwrotność - czyli taką liczbę, że te dwie wymnożone dają resztę 1 z dzielenia przez tę liczbę pierwszą. Napisz program, który odnajduje takie odwrotności. Wejście: Pierwsza linia wejścia zawiera dwie liczby całkowite Wyjście: Dla każdej liczby Przykład: Dla wejścia: 3 7 Poprawne wyjście to: 3 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Rozterki aptekarzaLimit czasowy: 1s; Limit pamięciowy: 16MB Aptekarz Joe chce odmierzyć Wejście: W pierwszej linii wejścia znajduje się jedna liczba całkowita Wyjście: Dla każdego zestawu testowego należy wypisać jedną linię, zawierającą najmniejszą liczbę odważników, potrzebnych do odważenia Przykład: Dla danych wejściowych: 2 Poprawne wyjście to: 2 Objaśnienie: Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (24 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 , oraz liczbę całkowitą dodatnią
, oraz liczbę całkowitą dodatnią  ,
, 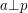 . Jak znaleźć taką liczbę całkowitą dodatnią
. Jak znaleźć taką liczbę całkowitą dodatnią  ,
, 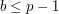 , taką, że
, taką, że 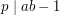 ?. (Taką liczbę nazywamy odwrotnością
?. (Taką liczbę nazywamy odwrotnością 
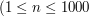 , oznaczającej ilość testów do rozważenia. W kolejnych
, oznaczającej ilość testów do rozważenia. W kolejnych 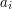 ,
, 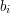
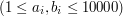 .
. 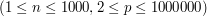 . W kolejnych n liniach znajduje się po jednej liczbie
. W kolejnych n liniach znajduje się po jednej liczbie 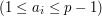 .
.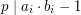 .
.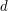 gramów substancji. Ma do dyspozycji dwa rodzaje odważników - o wadze
gramów substancji. Ma do dyspozycji dwa rodzaje odważników - o wadze 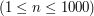 , oznaczające ilość zestawów testowych. W kolejnych
, oznaczające ilość zestawów testowych. W kolejnych 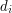 - największy wspólny dzielnik
- największy wspólny dzielnik 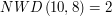 ,
, 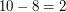 , więc potrzeba co najmniej dwóch odważników. W drugim przykładzie wystarczy jeden odważnik o wadze 1.
, więc potrzeba co najmniej dwóch odważników. W drugim przykładzie wystarczy jeden odważnik o wadze 1.

