Kolejny problem
Zastanówmy się nad rozwiązaniem poniższego zadania:
Aptekarz ma przed sobą ciężkie zadanie - musi odmierzyć  gramów leku, dysponuje dwoma odważnikami, o wagach
gramów leku, dysponuje dwoma odważnikami, o wagach  i
i  gramów. Może użyć dowolnej ilości każdego z tych odważników na wadze szalkowej. Znajdź sposób odważenia żądanej ilości leku.
gramów. Może użyć dowolnej ilości każdego z tych odważników na wadze szalkowej. Znajdź sposób odważenia żądanej ilości leku.

Przykładowe odważenie jedengo grama niebieskiego leku za pomocą odważników o wagach 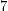 i
i 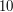 gramów.
gramów.
Jak się do tego zabrać? Postarajmy się zapisać to zadanie w języku matematyki:
Szukamy takich liczb całkowitych  i
i  , że:
, że:
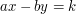
Zauważ, że nie ma sensu kłaść odważników tej samej wagi na różnych szalach - równoważyłyby się. Wobec tego możemy założyć, że układamy odważniki wagi  na lewej szalce, a odważniki wagi
na lewej szalce, a odważniki wagi  na prawej szalce. Wtedy różnica wag na obu szalkach musi być równa albo
na prawej szalce. Wtedy różnica wag na obu szalkach musi być równa albo  , albo
, albo 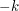 - oznacza to, że jeśli umieścimy lek odpowiednio na prawej bądź lewej szalce, waga będzie w stanie równowagi i odważymy szukane
- oznacza to, że jeśli umieścimy lek odpowiednio na prawej bądź lewej szalce, waga będzie w stanie równowagi i odważymy szukane  gramów.
gramów.
Zauważmy, że musi zachodzić 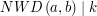 . W istocie, skoro
. W istocie, skoro 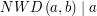 i
i 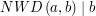 , to również
, to również 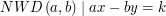 . Jeśli więc umielibyśmy znaleźć takie liczby
. Jeśli więc umielibyśmy znaleźć takie liczby  i
i 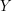 , że (przy oznaczeniu
, że (przy oznaczeniu 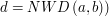
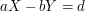
to biorąc 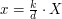 i
i 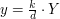 dostalibyśmy
dostalibyśmy
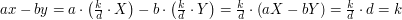
Okazuje się, że Algorytm Euklidesa potrafi znaleźć takie liczby.
Jeśli udałoby się znaleźć szukane liczby  i
i 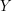 , to
, to 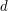 byłoby kombinacją liniową liczb
byłoby kombinacją liniową liczb  i
i  - to właśnie oznacza równanie
- to właśnie oznacza równanie 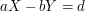 - liczbę d można zapisać jako sumę pewnej wielokrotności całkowitej liczby
- liczbę d można zapisać jako sumę pewnej wielokrotności całkowitej liczby  i pewnej wielokrotności całkowitej liczby
i pewnej wielokrotności całkowitej liczby  (nie przejmujmy się tym, że mamy minus - można by bez żadnej szkody napisać
(nie przejmujmy się tym, że mamy minus - można by bez żadnej szkody napisać 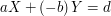 .
.
Zauważmy, że jeśli jakieś liczba 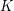 i
i 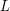 są kombinacjami liniowymi
są kombinacjami liniowymi  i
i  , to ich różnica,
, to ich różnica, 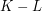 , również jest kombinacją liniową
, również jest kombinacją liniową  i
i  . Spójrzmy:
. Spójrzmy:
Jeśli 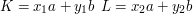 dla pewnych całkowitych
dla pewnych całkowitych 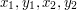 , to
, to 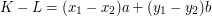 .
.
Jak działa Algorytm Euklidesa? Zaczynamy od 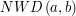 . Zarówno
. Zarówno  jak i
jak i  są oczywiście kombinacjami liniowymi
są oczywiście kombinacjami liniowymi  i
i  . W każdym kolejnym kroku algorytmu zamieniamy jedną z tych liczb na ich różnicę. Wobec tego cały czas algorytm pracuje na dwóch liczbach, będących kombinacjami liniowymi
. W każdym kolejnym kroku algorytmu zamieniamy jedną z tych liczb na ich różnicę. Wobec tego cały czas algorytm pracuje na dwóch liczbach, będących kombinacjami liniowymi  i
i  . W końcu docieramy do
. W końcu docieramy do 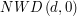 - wobec tego
- wobec tego 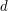 też jest kombinacją liniową
też jest kombinacją liniową  i
i  . Spójrzmy na przykład:
. Spójrzmy na przykład:
Niech 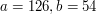
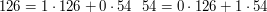
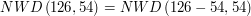
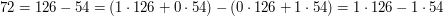
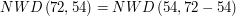
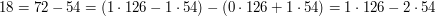
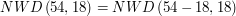
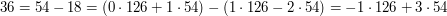
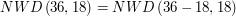
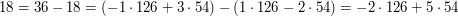
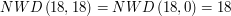
Udało się! Nie dość, że znaleźliśmy 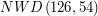 , równe
, równe 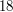 , to wiemy, że
, to wiemy, że 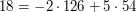 . Zauważ, że policzyliśmy też krok wcześniej w algorytmie, że
. Zauważ, że policzyliśmy też krok wcześniej w algorytmie, że 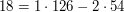 . Widzimy więc, że takie przedstawienie w postaci kombinacji liniowej nie jest unikalne. Zajmiemy się tą sprawą w dalszej części algorytmu, teraz postarajmy się wyprowadzić sposób na obliczanie współczynników
. Widzimy więc, że takie przedstawienie w postaci kombinacji liniowej nie jest unikalne. Zajmiemy się tą sprawą w dalszej części algorytmu, teraz postarajmy się wyprowadzić sposób na obliczanie współczynników  i
i 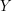 do równania
do równania 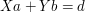 . Przy okazji warto byłoby też przekształcić powyższy przykład do ulepszonego algorytmu Euklidesa - tego, w którym zamiast odejmować liczby od siebie wielokrotnie, od razu "wycinaliśmy" wszystkie wystąpienia mniejszej liczby z większej liczby.
. Przy okazji warto byłoby też przekształcić powyższy przykład do ulepszonego algorytmu Euklidesa - tego, w którym zamiast odejmować liczby od siebie wielokrotnie, od razu "wycinaliśmy" wszystkie wystąpienia mniejszej liczby z większej liczby.
Nie będzie to dużo trudniejsze - spójrzmy na ten sam przykład:
Niech 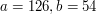
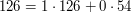
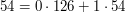
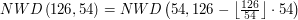
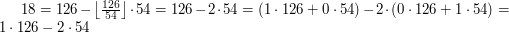
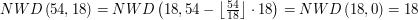
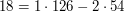
Poniżej przykład dla 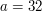 i
i 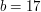 :
:
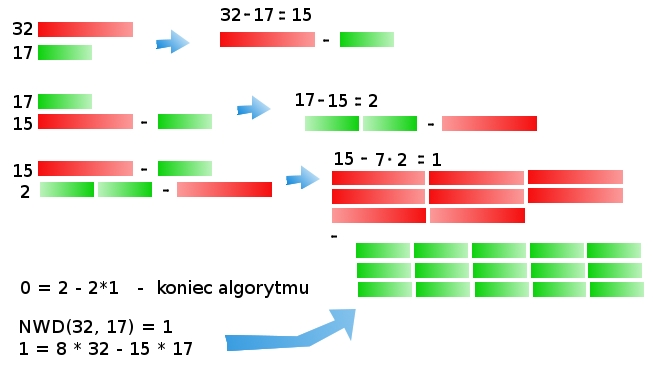
Algorytm
O ileż szybciej! Wprowadźmy pewne oznaczenia, aby móc łatwo zapisać tę zależność algorytmem:
1. Oznaczmy kolejne liczby pojawiające się w Algorytmie Euklidesa, jako 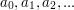 . Mamy na myśli to, że
. Mamy na myśli to, że 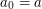 ,
, 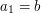 ,
, 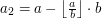 i tak dalej...
i tak dalej...
2. Niech ciągi 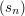
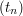 spełniają zależności:
spełniają zależności:
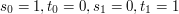
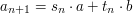
Co to oznacza? Liczby 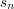 i
i 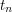 to współczynniki, które pozwalają przedstawić kolejne liczby pojawiające się w algorytmie Euklidesa jako kombinacje liniowe
to współczynniki, które pozwalają przedstawić kolejne liczby pojawiające się w algorytmie Euklidesa jako kombinacje liniowe  i
i  . Mamy więc dla naszego powyższego przykładu:
. Mamy więc dla naszego powyższego przykładu:
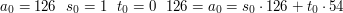
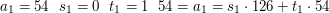
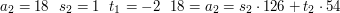
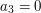 - Koniec algorytmu
- Koniec algorytmu
Widzimy wobec tego, że gdy algorytm się zakończy ( dla pewnego 
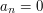 ) to współczynniki, których szukamy, to
) to współczynniki, których szukamy, to 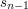 i
i 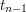 - one spełniają
- one spełniają 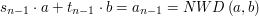 gdyż wiemy, że gdy osiągamy zero dla
gdyż wiemy, że gdy osiągamy zero dla 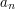 , to poprzednio uzyskana liczba
, to poprzednio uzyskana liczba 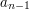 jest największym współnym dzielnikiem
jest największym współnym dzielnikiem  i
i  .
.
Jak obliczać te współczynniki? Spójrzmy poniżej:
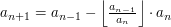
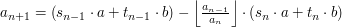
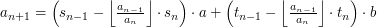
Więc jeśli przyjmiemy:
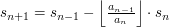
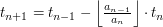
to otrzymamy:
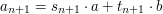 Hurra!
Hurra!
Przyjżyjmy się poniższemu algorytmowi:
int a[1000], s[1000], t[1000];
int A, B, n, q, temp;
cin >> A >> B;
a[0] = A;
a[1] = B;
s[0] = 1; s[1] = 0;
t[0] = 0; t[1] = 1;
n = 1;
while(a[n] != 0){
q = a[n-1]/a[n];
a[n+1] = a[n-1] - q*a[n];
s[n+1] = s[n-1] - q*s[n];
t[n+1] = t[n-1] - q*t[n];
n++;
}
cout << "NWD(" << A << "," << B << ") = " << a[n-1] << endl;
cout << s[n-1] << "*" << A << " + ";
cout << t[n-1] << "*" << B << " = " << a[n-1] << endl;
Wypróbuj go! Zastanów się, dlaczego tablice o rozmiarze 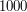 na pewno wystarczą. Zastanów się też, czy nie dałoby się zapisać tego algorytmu z mniejszym zużyciem pamięci - nie deklarując tablic (zwróć uwagę na to, że np. gdy już obliczysz
na pewno wystarczą. Zastanów się też, czy nie dałoby się zapisać tego algorytmu z mniejszym zużyciem pamięci - nie deklarując tablic (zwróć uwagę na to, że np. gdy już obliczysz ![$ a\left[10\right], s\left[10\right] $](/files/tex/1768ee31bb252f7665df3f5b4ef6c4c713117d27.png) i
i ![$ t\left[10\right] $](/files/tex/a03477ef563d4278725b163054f9c8f2262c6a8d.png) , to nigdy nie będziesz korzystać z
, to nigdy nie będziesz korzystać z ![$ a\left[0\right], a\left[1\right], \ldots , a\left[8\right] $](/files/tex/309b989251a3035f37934fb80bed435b1269541f.png) ,
, ![$ s\left[0\right], s\left[1\right], \ldots , s\left[8\right] $](/files/tex/6a8d658bd37ec51824436f685647dc109b4d4855.png) ,
, ![$ t\left[0\right], t\left[1\right], \ldots , t\left[8\right] $](/files/tex/1aba7991f58538556df8984a41a0b4fcf88d696a.png) .
.
Kilka ciekawych problemów
W jednym z naszych przykładów okazało się, że 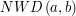 można zapisać jako kombinację liniową
można zapisać jako kombinację liniową  i
i  na wiele sposobów. Jak wyzaczyć wszystkie takie sposoby?
na wiele sposobów. Jak wyzaczyć wszystkie takie sposoby?
Załóżmy, że:
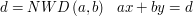
Weźmy 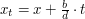 ,
, 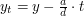 dla liczby całkowitej
dla liczby całkowitej  .
.
Wtedy 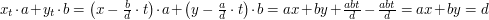
Wobec tego dla każdego  całkowitego
całkowitego 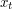 i
i 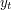 też są dobrymi współczynnikami, pozwalającymi uzyskać
też są dobrymi współczynnikami, pozwalającymi uzyskać 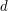 jako kombinację liniową
jako kombinację liniową  i
i  . Znaleźliśmy nieskończenie wiele takich liczb. Ale czy to wszystkie takie liczby?
. Znaleźliśmy nieskończenie wiele takich liczb. Ale czy to wszystkie takie liczby?
Załóżmy przeciwnie - że można znaleźć takie dwie liczby całkowite  ,
, 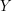 , że nie różnią się od naszych
, że nie różnią się od naszych  i
i  o odpowiednio wielokrotność
o odpowiednio wielokrotność  i
i 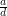 . Mielibyśmy wtedy:
. Mielibyśmy wtedy:
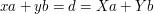
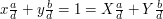
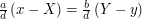
Ale  i
i 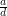 są względnie pierwsze (inaczej
są względnie pierwsze (inaczej 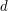 nie byłoby największym dzielnikiem). Wobec tego musi zachodzić:
nie byłoby największym dzielnikiem). Wobec tego musi zachodzić:

A to oznacza, że muszą się różnić o wielokrotność odpowiednio 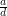 i
i  , co dowodzi, że nasz sposób znajduje wszystkie rozwiązania.
, co dowodzi, że nasz sposób znajduje wszystkie rozwiązania.



 gramów leku, dysponuje dwoma odważnikami, o wagach
gramów leku, dysponuje dwoma odważnikami, o wagach  i
i  gramów. Może użyć dowolnej ilości każdego z tych odważników na wadze szalkowej. Znajdź sposób odważenia żądanej ilości leku.
gramów. Może użyć dowolnej ilości każdego z tych odważników na wadze szalkowej. Znajdź sposób odważenia żądanej ilości leku.
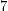 i
i 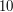 gramów.
gramów. i
i  , że:
, że: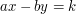
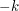 - oznacza to, że jeśli umieścimy lek odpowiednio na prawej bądź lewej szalce, waga będzie w stanie równowagi i odważymy szukane
- oznacza to, że jeśli umieścimy lek odpowiednio na prawej bądź lewej szalce, waga będzie w stanie równowagi i odważymy szukane 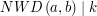 . W istocie, skoro
. W istocie, skoro 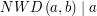 i
i 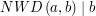 , to również
, to również 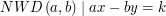 . Jeśli więc umielibyśmy znaleźć takie liczby
. Jeśli więc umielibyśmy znaleźć takie liczby  i
i 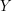 , że (przy oznaczeniu
, że (przy oznaczeniu 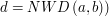
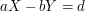
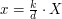 i
i 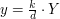 dostalibyśmy
dostalibyśmy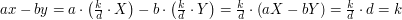
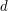 byłoby kombinacją liniową liczb
byłoby kombinacją liniową liczb 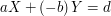 .
.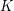 i
i 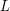 są kombinacjami liniowymi
są kombinacjami liniowymi 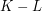 , również jest kombinacją liniową
, również jest kombinacją liniową 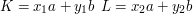 dla pewnych całkowitych
dla pewnych całkowitych 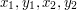 , to
, to 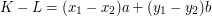 .
.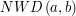 . Zarówno
. Zarówno 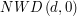 - wobec tego
- wobec tego 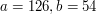
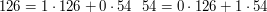
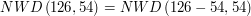
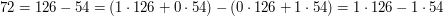
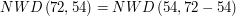
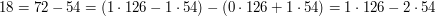
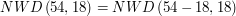
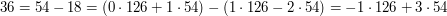
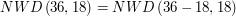
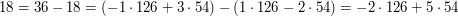
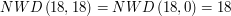
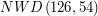 , równe
, równe 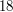 , to wiemy, że
, to wiemy, że 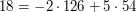 . Zauważ, że policzyliśmy też krok wcześniej w algorytmie, że
. Zauważ, że policzyliśmy też krok wcześniej w algorytmie, że 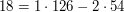 . Widzimy więc, że takie przedstawienie w postaci kombinacji liniowej nie jest unikalne. Zajmiemy się tą sprawą w dalszej części algorytmu, teraz postarajmy się wyprowadzić sposób na obliczanie współczynników
. Widzimy więc, że takie przedstawienie w postaci kombinacji liniowej nie jest unikalne. Zajmiemy się tą sprawą w dalszej części algorytmu, teraz postarajmy się wyprowadzić sposób na obliczanie współczynników 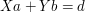 . Przy okazji warto byłoby też przekształcić powyższy przykład do ulepszonego algorytmu Euklidesa - tego, w którym zamiast odejmować liczby od siebie wielokrotnie, od razu "wycinaliśmy" wszystkie wystąpienia mniejszej liczby z większej liczby.
. Przy okazji warto byłoby też przekształcić powyższy przykład do ulepszonego algorytmu Euklidesa - tego, w którym zamiast odejmować liczby od siebie wielokrotnie, od razu "wycinaliśmy" wszystkie wystąpienia mniejszej liczby z większej liczby.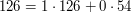
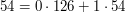
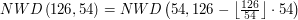
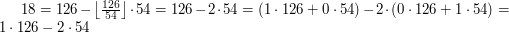
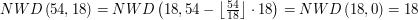
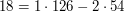
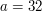 i
i 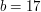 :
:
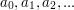 . Mamy na myśli to, że
. Mamy na myśli to, że 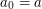 ,
, 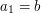 ,
, 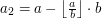 i tak dalej...
i tak dalej... 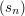
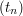 spełniają zależności:
spełniają zależności: 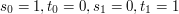
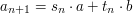
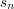 i
i 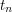 to współczynniki, które pozwalają przedstawić kolejne liczby pojawiające się w algorytmie Euklidesa jako kombinacje liniowe
to współczynniki, które pozwalają przedstawić kolejne liczby pojawiające się w algorytmie Euklidesa jako kombinacje liniowe 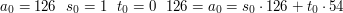
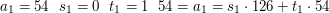
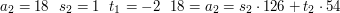
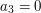 - Koniec algorytmu
- Koniec algorytmu
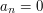 ) to współczynniki, których szukamy, to
) to współczynniki, których szukamy, to 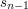 i
i 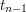 - one spełniają
- one spełniają 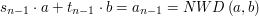 gdyż wiemy, że gdy osiągamy zero dla
gdyż wiemy, że gdy osiągamy zero dla 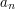 , to poprzednio uzyskana liczba
, to poprzednio uzyskana liczba 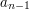 jest największym współnym dzielnikiem
jest największym współnym dzielnikiem 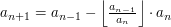
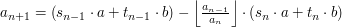
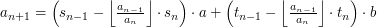
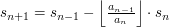
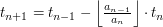
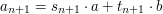 Hurra!
Hurra!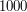 na pewno wystarczą. Zastanów się też, czy nie dałoby się zapisać tego algorytmu z mniejszym zużyciem pamięci - nie deklarując tablic (zwróć uwagę na to, że np. gdy już obliczysz
na pewno wystarczą. Zastanów się też, czy nie dałoby się zapisać tego algorytmu z mniejszym zużyciem pamięci - nie deklarując tablic (zwróć uwagę na to, że np. gdy już obliczysz ![$ a\left[10\right], s\left[10\right] $](/files/tex/1768ee31bb252f7665df3f5b4ef6c4c713117d27.png) i
i ![$ t\left[10\right] $](/files/tex/a03477ef563d4278725b163054f9c8f2262c6a8d.png) , to nigdy nie będziesz korzystać z
, to nigdy nie będziesz korzystać z ![$ a\left[0\right], a\left[1\right], \ldots , a\left[8\right] $](/files/tex/309b989251a3035f37934fb80bed435b1269541f.png) ,
, ![$ s\left[0\right], s\left[1\right], \ldots , s\left[8\right] $](/files/tex/6a8d658bd37ec51824436f685647dc109b4d4855.png) ,
, ![$ t\left[0\right], t\left[1\right], \ldots , t\left[8\right] $](/files/tex/1aba7991f58538556df8984a41a0b4fcf88d696a.png) .
.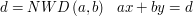
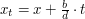 ,
, 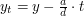 dla liczby całkowitej
dla liczby całkowitej  .
.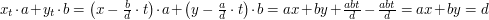
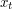 i
i 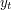 też są dobrymi współczynnikami, pozwalającymi uzyskać
też są dobrymi współczynnikami, pozwalającymi uzyskać  i
i 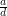 . Mielibyśmy wtedy:
. Mielibyśmy wtedy: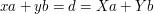
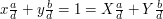
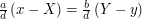
 i
i 


