Algorytm Euklidesa
31.10.2009 - Damian Rusak
 Znajdowanie największego wspólnego dzielnikaWiemy już, że pozostało nam znaleźć sposób na obliczanie największego wspólnego dzielnika. Wiemy już pewną bardzo ważną rzecz - jeśli jakaś liczba Jeśli Dlaczego? Wiemy już, że jeśli jakaś liczba dzieli Stąd już tylko parę kroków do zachwycającego prostotą algorytmu Euklidesa. Prześledźmy wykorzystanie faktu
Uff... trochę to przydługawe, ale w końcu dobrnęliśmy do rozwiązania - To, co wykonaliśmy powyżej, to właśnie Algorytm Euklidesa. Dopóki jedna z liczb Jeszcze lepiejOczywiście da się ten algorytm ulepszyć. Zauważ, że trochę bez sensu było liczenie kolejno W takim razie nietrudno jest ulepszyć nasz algorytm do takiej postaci:
Wyjaśnijmy sobie to! Zauważ, jak przyspiesza to działanie algorytmu - gdybyśmy chcieli poprzednią metodą liczyć Zapiszmy nasz algorytm w języku C++: int NWD(int a, int b){
Jest to dokładnie zapis naszego algorytmu - dopóki mniejszy z elementów pary Jak szybko działa ten algorytm? Jeżeli znane są Ci pojęcia złożoności obliczeniowej to zapewne ucieszy Cię wiadomość, że Algorytm Euklidesa działa w czasie logarytmicznym względem wielkości liczb Zachęcamy do zapisania tego algorytmu i wykorzystania go do rozwiązania zadania Monety. Jego dokładna treść i specyfikacja znajdują się na ostatniej stronie artykułu. (24 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


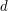 dzieli
dzieli  i dzieli
i dzieli  , to dzieli również ich różnicę,
, to dzieli również ich różnicę, 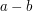 . W szczególności dotyczy to
. W szczególności dotyczy to 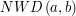 . Mamy więc:
. Mamy więc: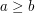 to
to 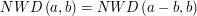
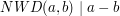 . Z kolei wiemy też, że każdy wspólny dzielnik dwóch liczb dzieli ich sumę, stąd
. Z kolei wiemy też, że każdy wspólny dzielnik dwóch liczb dzieli ich sumę, stąd 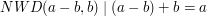 . Wobec tego zachodzi powyższa równość, bo każdy wspólby dzielnik
. Wobec tego zachodzi powyższa równość, bo każdy wspólby dzielnik 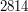 i
i 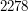 :
: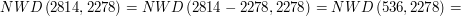
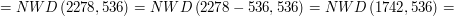
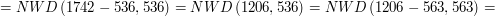
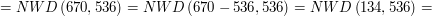
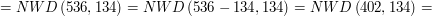
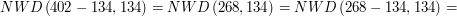
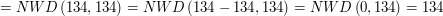
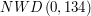 musi być równe
musi być równe 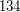 , gdyż
, gdyż  dzieli się przez każdą niezerową liczbę, więc też przez
dzieli się przez każdą niezerową liczbę, więc też przez 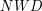 jest równe poprzedniemu, a kiedyś musimy dobrnąć do zera (dlaczego?) i odnaleźć rozwiązanie, gdyż jeśli
jest równe poprzedniemu, a kiedyś musimy dobrnąć do zera (dlaczego?) i odnaleźć rozwiązanie, gdyż jeśli 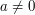 , to
, to 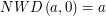 .
.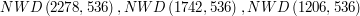 ,
, 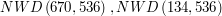 . Cały czas odejmowaliśmy
. Cały czas odejmowaliśmy 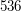 , aż osiągnęliśmy liczbę mniejszą niż
, aż osiągnęliśmy liczbę mniejszą niż 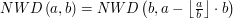
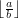 to wynik dzielenia
to wynik dzielenia 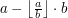 to właśnie wynik odjęcia od
to właśnie wynik odjęcia od 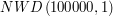 ... Tymczasem w naszej nowej metodzie mamy
... Tymczasem w naszej nowej metodzie mamy 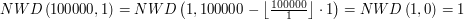 .
.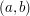 nie jest zerem, wykonujemy "zamianę"
nie jest zerem, wykonujemy "zamianę" 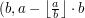 . Gdy
. Gdy 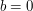 , nasz największy wspólny dzielnik to
, nasz największy wspólny dzielnik to 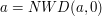 .
.

