Drukarka, czyli kłamstwa Twoich oczu

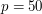Wynik zastosowania poprzedniego algorytmu (przy ).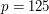

Wynik zastosowania poprzedniego algorytmu (przy ).

Wynik zastosowania poprzedniego algorytmu (przy ).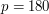

Skomplikowana propagacja błędu

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

U = obrazek wejściowy
T = obrazek z szumem
p = parametr algorytmu
Dla i = 1...n
 Dla j = 1..m
  Jeżeli U[i,j] > p
   T[i,j] = 255
  W przeciwnym razie:
   T[i,j] = 0 
  błąd = U[i,j] - T[i,j]
  U[i,j+1] += 4/21 błąd
  U[i,j+2] += 2/21 błąd
  U[i+1,j-2] += 1/21 błąd
  U[i+1,j-1] += 2/21 błąd  
  U[i+1,j]   += 4/21 błąd    
  U[i+1,j+1] += 2/21 błąd      
  U[i+1,j+2] += 1/21 błąd        
  U[i+2,j-2] += 1/42 błąd
  U[i+1,j-1] += 1/21 błąd  
  U[i+1,j]   += 2/21 błąd    
  U[i+1,j+1] += 1/21 błąd      
  U[i+1,j+2] += 1/42 błąd        

Ten algorytm działa tak samo jak poprzedni, ale rozdziela błąd na większą liczbę sąsiadów.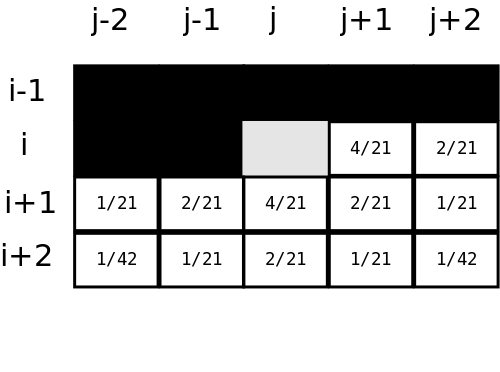

Schemat skomplikowanej propagacji błędu. Czarne pola już przetworzyliśmy i nie możemy ich już modyfikować. Szare pole właśnie przetwarzamy. Liczba oznacza jaką część błędy przydzielamy temu polu. Ważne jest, że wszystkie ułamki sumują się do jedynki - chcemy rodzielić cały błąd!

Wynik zastosowania algorytmu skomplikowanej propagacji błędu (przy ).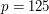

Uwaga o tym, że nie wszyscy mają w życiu równie lekko

Ostatni algorytm dał całkiem niezłe wyniki. Ale czy są wystarczająco dobre? Musicie wiedziecie, że wasza drukarka ma trochę prostsze zadanie, niż mogłoby się wydawać w pierwszej chwili. A to dlatego, że rozdzielczość drukarki (nawet atramentowej!) jest dużo większa niż monitora. To znaczy: piksel na monitorze jest zazwyczaj większy od kropel, które drukarka nanosi na papier. Dlatego ostatni algorytm w rzeczywistości już całkiem nieźle nadaje się do stosowania w drukarkach. Sprawdźcie sami! Zamiast drukować te zdjęcia możecie na przykład odejść parę kroków od monitora.

Możecie też sami poszukać najlepszych współczynników dla algorytmu za pomocą programu, który jest na następnej, ostatniej stronie tego artykułu.