Drukarka, czyli kłamstwa Twoich oczu
23.11.2009 - Krzysztof Dryś
  SzumZazwyczaj nie chcemy mieć na naszych zdjęciach szumów. Przekonamy się jednak, że mogą one być przydatne. Najpierw jednak zobaczymy jak sami możemy generować szum.
Wyobraźmy sobie, że mamy do dyspozycji kostkę 5 ścienną. Na jej ścianach wymalowane są liczby -2,-1,0,1,2. Gdy rzucamy kostką, każda ściana może wypaść z jednakowym prawdopodobieństwem. Innymi słowy, jeżeli oznaczymy wynik rzutu kostką jako
Czy wiesz, że: tak zdefiniowany
 jest dyskretną zmienną losową o rozkładzie jednostajnym? Ta wiedza zupełnie nie będzie nam potrzebna, ale świetnie nadaje się do imponowania znajomym! jest dyskretną zmienną losową o rozkładzie jednostajnym? Ta wiedza zupełnie nie będzie nam potrzebna, ale świetnie nadaje się do imponowania znajomym!
Nasza kostka nie musi mieć akurat 5 ścian. Równie dobrze możemy sobie wyobrazić, że mamy kostkę, która ma
Ale tak właściwie - kto by się bawił kostkami w epoce komputerów? Zamiast kostki możemy wziąć funkcję kostka(d). Wyjściem tej funkcji jest wynik rzutu kostką No, dobrze, ale jaki ma to związek z szumem? Otóż ta funkcja bardzo przyda się nam do zbudowaniu algorytmu zaszumiającego obrazek:
Popatrzmy na obrazki, wyprodukowane przez ten algorytm.  Wynik zastosowania algorytmu przy
Wynik zastosowania algorytmu przy 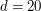 . .
 Wynik zastosowania algorytmu przy
Wynik zastosowania algorytmu przy 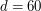 . .
 Wynik zastosowania algorytmu przy
Wynik zastosowania algorytmu przy 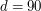 . .
Co widzimy na powyższych obrazkach? Im większe Pamiętacie jeszcze, że naszym celem jest stworzenie obrazka, który będzie mogła wydrukować drukarka? Okazuje się, że szum może nam pomóc. Spróbujmy zastosować poprzedni algorytm na zaszumionych obrazkach.  Wynik zastosowania pierwszego algorytmu (przy
Wynik zastosowania pierwszego algorytmu (przy 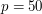 ) na zaszumionym obrazku (przy ) na zaszumionym obrazku (przy 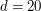 ). ).
 Wynik zastosowania pierwszego algorytmu (przy
Wynik zastosowania pierwszego algorytmu (przy 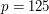 ) na zaszumionym obrazku (przy ) na zaszumionym obrazku (przy 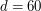 ). ).
 Wynik zastosowania pierwszego algorytmu (przy
Wynik zastosowania pierwszego algorytmu (przy 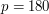 ) na zaszumionym obrazku (przy ) na zaszumionym obrazku (przy 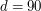 ). ).
(9 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


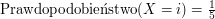 dla
dla 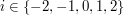 .
.
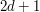 ścian. Na tych ścianach będą liczby -d, -(d-1) ... -1,0,1 ... (d-1), d . Teraz
ścian. Na tych ścianach będą liczby -d, -(d-1) ... -1,0,1 ... (d-1), d . Teraz 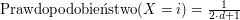 dla
dla 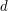 , tym więcej jest szumu. A to dlatego, że większy jest rozrzut wartości zwracanych przez funkcję kostka(d).
, tym więcej jest szumu. A to dlatego, że większy jest rozrzut wartości zwracanych przez funkcję kostka(d).


