Od programowania do kafelkowania (i z powrotem)
16.10.2009 - Krzysztof Dryś
   Od Maszyny Turinga do kafelkówNo nareszcie - zbudowaliśmy opis komputera. Czas spożytkować nasz trud i użyć tego opisu do pokazania czegoś naprawdę ciekawego. Zobaczymy jak za pomocą kafelków zasymulować Maszynę Turinga. Tak właśnie! Zobaczymy jak można przeprowadzać obliczenia na kafelkach łazienkowych. Jak to możliwe? Idea będzie następująca: Kolejne rzędy kafelków będą oznaczać stan taśmy Maszyny Turinga w kolejnych krokach. Najpierw popatrzmy na kafelki. Każdy kafelek będzie odpowiadał jednemu polu na taśmie i będzie zawierał dwie informacje:
Przełóżmy to na język kafelków. Na każdym kafelku jest wzorek. Składa się on z dwóch elementów. Dolna połowa mówi jaki symbol jest zapisany na polu, któremu odpowiada kafelek. Jeżeli nad polem nie ma głowicy, to górne pole jest puste. Jeżeli nad polem jest głowica, to na górnym polu znajduje się numer tego stanu. 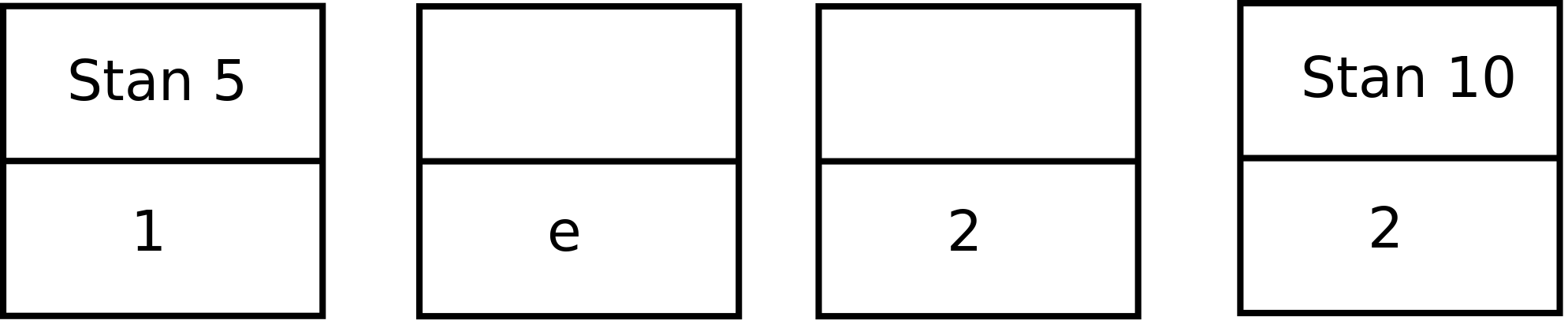 Na obrazkach widać przykładowe kafelki. Ich znaczenie to:
Na obrazkach widać przykładowe kafelki. Ich znaczenie to:
Informacje o tym, co robi (tzn. jak się przemieszcza i co pisze) głowica w kolejnych stanach będziemy kodowali za pomocą dozwolonych kwadratów. Wreszcie początkowy stan maszyny będzie zakodowany jako kompozycja, której zażyczył sobie artysta na górny rząd kafelków. 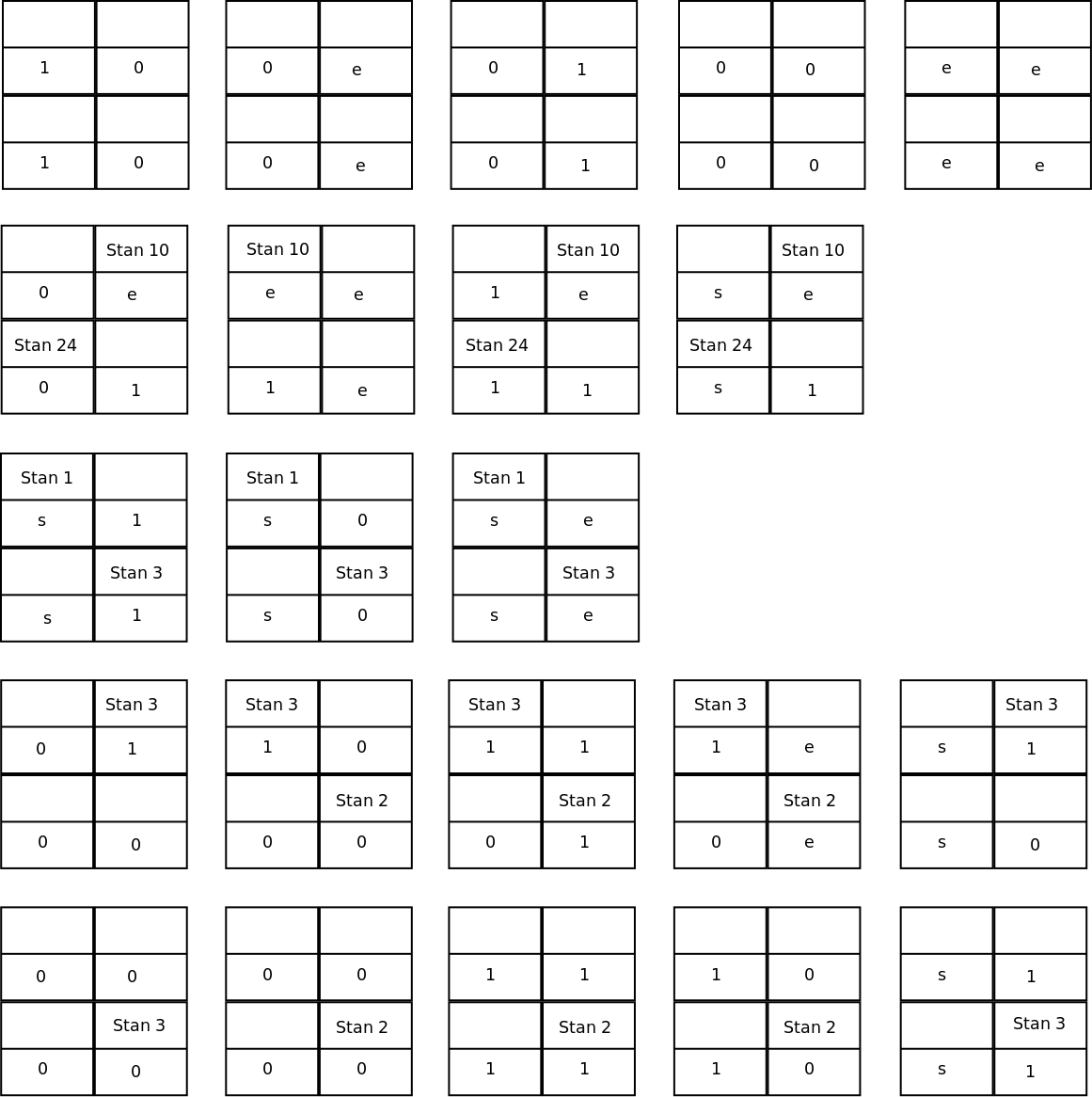 Przykład zakodowania reguł pewnej Maszyny Turinga jako dozwolonych kafelków. W kolejnych wierszach widzimy następujące reguły:
Przykład zakodowania reguł pewnej Maszyny Turinga jako dozwolonych kafelków. W kolejnych wierszach widzimy następujące reguły:
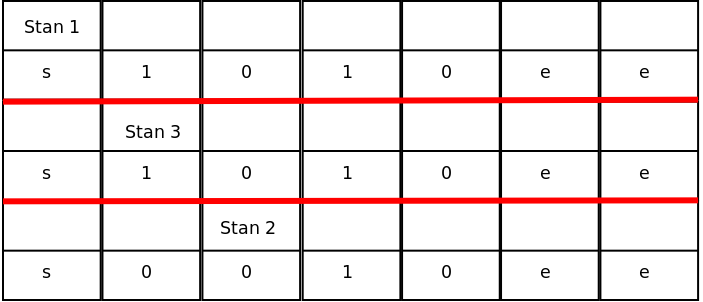 Przykład trzech kolejnych stanów Maszyny Turinga zakodowanych za pomocą kafelków.
Przykład trzech kolejnych stanów Maszyny Turinga zakodowanych za pomocą kafelków.
Oto istota całego dowodu -- ścianę da się wykafelkować wtedy i wtedy, gdy Maszyna Turinga się zatrzymuje!
Pozostaje pokazać dwie rzeczy:
(5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 . Nad polem jest głowica, która znajduje się w stanie 5.
. Nad polem jest głowica, która znajduje się w stanie 5.  . Nad polem nie ma głowicy.
. Nad polem nie ma głowicy.  . Nad polem nie ma głowicy.
. Nad polem nie ma głowicy.  , to nie nie pisz, przejdź w stan 3 idź w prawo
, to nie nie pisz, przejdź w stan 3 idź w prawo , przejdź w stan 2 i idź w prawo
, przejdź w stan 2 i idź w prawo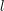 , to według podanych zasad da się wykafelkować ścianę,
, to według podanych zasad da się wykafelkować ścianę,

