Od programowania do kafelkowania (i z powrotem)
16.10.2009 - Krzysztof Dryś
   Ważne twierdzenie (bez dowodu)Czy Maszyna Turinga jest dobry modelem dla komputerów? Jest. Świadczy o tym następujące twierdzenie: Dla każdego programu istnieje równoważna mu Maszyna Turinga. Dla każdej Maszyny Turinga istnieje równoważny jej program.
Mówimy, że program się zapętlił, jeżeli jest w takim stanie, że nigdy nie zakończy obliczeń i nigdy nie zwróci wyniku.
Co to znaczy, że program Ważne twierdzenie (z innego artykułu)Czytaliście artykuł o tym, czy komputery mogą wszystko? Można tam zobaczyć między innymi następuje twierdzenie:
Nie da się napisać programu, który czyta kod innego programu oraz liczbę Twierdzenie o Maszynie TuringaSpróbujmy dowiedzieć się czegoś o Maszynie Turinga. Pokażemy następujące twierdzenie:
Nie istnieje program, który czyta na wejściu opis Maszyny Turinga oraz liczbę
To jak będziemy kodować, czyli pamiętać w komputerze Maszynę Turinga zupełnie nas tutaj nie obchodzi!
To twierdzenie mówi o nowym ograniczeniu komputerów. Do tej pory wiedzieliśmy, że nie da się sprawdzić, czy jakiś program się może się zatrzymać. Teraz zobaczymy, że nie da się również sprawdzić, czy Maszyna Turinga może się zatrzymać !
Przeprowadzimy prosty dowód nie wprost. Załóżmy, że istnieje program, który czyta na wejściu opis Maszyny Turinga oraz liczbę
Program Innymi słowy - taki algorytm nie istnieje. To twierdzenie jest ciekawe - mówi nam coś nowego o komputerach. Ale zaraz będzie jeszcze ciekawiej. Nareszcie dowiemy się czegoś o kafelkowaniu! (5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 jest równoważny maszynie
jest równoważny maszynie 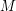 ? Oznacza to, że dla każdych danych wejściowych program
? Oznacza to, że dla każdych danych wejściowych program 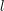 i mówi, czy ten program zapętli się po przeczytaniu liczby
i mówi, czy ten program zapętli się po przeczytaniu liczby 

